The Gompertz Sigmoid Function and Its Derivative

Gompertz function - green; derivative - gray; logarithmic derivative - orange

upper asymptote a

3.69

growth rate b

-2.4

growth rate c

-1.825

filling

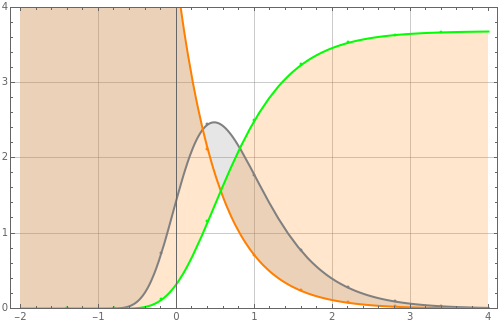
This Gompertz function is defined by

f(t)=a

b

ct

e

or

f(t)=aexp(bexp(ct))

, where

a

is the upper asymptote and

b

and

c

are the negative growth rates. The Gompertz function is a sigmoid function. It is a type of mathematical model for a time series, where growth is slowest at the start and end of a time period. This Demonstration plots the Gompertz function

f(t)

, its derivative,

f'(t)=abc

b

ct

e

ct

e

, and the ratio

d

dt

ln(f(t)

)=

f'(t)/f(t)

.

Details

For more information, see the Wikipedia entry for Gompertz–Makeham Law of Mortality, as well as B. Gompertz, "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies," Philosophical Transactions of the Royal Society of London, 115, 1825 pp. 513–585.

External Links

Gompertz Curve (Wolfram MathWorld)

Permanent Citation

Olexandr Eugene Prokopchenko

"The Gompertz Sigmoid Function and Its Derivative"
http://demonstrations.wolfram.com/TheGompertzSigmoidFunctionAndItsDerivative/
Wolfram Demonstrations Project
Published: March 7, 2011