Epsilon-Delta Definition of Limit
Epsilon-Delta Definition of Limit
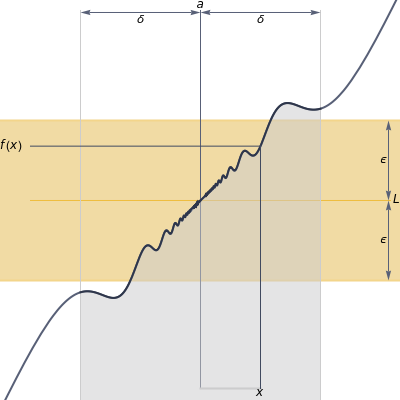
One of the key concepts of calculus is the limit of a function. Informally, a function has a limit at a point if the value gets close to a fixed number as gets close to . This Demonstration illustrates a more formal definition of limit, usually referred to as the - definition. The arrangement of the sliders highlights the importance of the wording of the definition.
f:
L
a
f(x)
L
x
a
ϵ
δ
Details
Details
Snapshot 1: is not yet small enough for the previously chosen
δ
ϵ
Snapshot 2: discontinuous function, but one-sided limits exist
Snapshot 3: a function with no limit (with zoom); for the on this snapshot, no works
ϵ
δ
External Links
External Links
Permanent Citation
Permanent Citation
Ferenc Beleznay
"Epsilon-Delta Definition of Limit"
http://demonstrations.wolfram.com/EpsilonDeltaDefinitionOfLimit/
Wolfram Demonstrations Project
Published: June 24, 2014