微分とは何か?-AI時代の学び方―
微分とは何か?-AI時代の学び方―
今は、微分も積分もAIが正解を出す時代だ。だからこそ、正解を出す機械を扱う技術を得て、より本質を理解する事が現代に求められるのではないか。そんな学び方を、今回は微分を例に紹介したい。
関数とは何か?
関数とは何か?
自由落下(フリーフォール)の関数
自由落下(フリーフォール)の関数
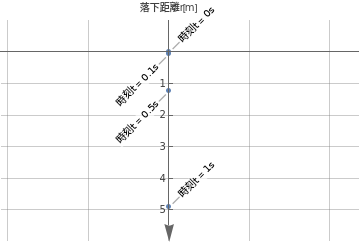
関数の例として、物体の落下を紹介しよう。時刻 [s]における落下距離 [m]を関数 として以下のようにあらわす。
いくつか例を計算し、関数に慣れよう。
t
r
r(t)
r(t)4.9tt4.9
2
t
いくつか例を計算し、関数に慣れよう。
例1:時刻 における落下距離は、定義の数式の通りにを代入して掛け算すると、 と正解が出る。落下距離0m、つまり落下していないと分かる。
t0
r(0)
r(t)4.9tt
t0
r(0)4.9000
例2:時刻 s (=1秒)における距離は と正解が出る。つまり落下距離4.9m(=4.9メートル)と分かる。
t1
r(1)4.9114.9
このように関数は、下の表のように定義の数式に入力値(Input)を代入し掛け算するだけだ。
定義 | r(t)4.9tt |
入力 | 時刻 t |
計算 | 代入し2回掛け算 |
出力 | 落下距離 r |
計算は電卓にやらせればよいが、次は Mathematica に正解を出力させよう。数式に似た記述をすれば、代入や掛け算をしてくれる。
例3:時刻 s における距離 の正解を、Mathematica に出力させる。
t0.5
r(0.5)
r[t_]:=4.9;(*関数の定義。定義では:=を使い、入力変数はアンダーバーを付けt_と区別する*)r[0.5](*定義された関数r[t]へ入力値t=0.5を代入*)
2
t
Out[]=
1.225
出力(Output)の値が 1.225 なので、時刻t=0から0.5秒間で約1.2m 落下するのが分かる。同様に、0.1秒間で落下距離 0.049m=4.9 cm となる。0.1秒も0.5秒も、人間には「一瞬」と認知されるが、落下距離はそれぞれ4.9cmと約1.2mとなり大きな差だ。このように物理現象を正確に理解できるのも、中学で習う「関数」のおかげだ。
例4:念のために、時刻 s における距離 の正解が0.049mかどうか、Mathematica に出力させよう。
t0.1
r(0.1)
In[]:=
r[0.1](*定義された関数r[t]へ今度は入力値t=0.1を代入*)
Out[]=
0.049
正解0.049を出力している。例3にあった「関数の定義 r[t_]:= ... 」の記述は、既にMathematicaに覚えさせた状態になっているため省略できる。このような再利用可能性も、関数の利便性の一つだ。
以上で扱った時刻 に対し、縦軸を落下距離に取ると以下のように図示できる。
t
Out[]=
実は、四則演算も関数(2変数関数)
実は、四則演算も関数(2変数関数)
先ほどは、「掛け算」を2回するだけなので小学校算数レベルだった。通常、四則演算は演算記号(など)を二つの数a,bの間に表記し、例えば引き算を と表現する(中間記法と呼ぶ)。実は、この四則演算も、 実は「関数」である。Mathematicaでは、関数名( Plus, Subtract, Times, Divideなど)を先頭に表記し、続いて数a,b を二つ記述しても同じである。
+,-,,÷
a-b
In[]:=
Subtract[a,b] (*関数Subtractは引き算(減算)をする*)
Out[]=
a-b
先ほど定義した r[t] は入力する変数が1つなので「1変数関数」であり、この Subtract[a,b] は入力変数がaとbの2つなので「2変数関数」と呼ぶ。2変数関数の出力値は、2つの入力変数a,b の両方の値に依存して変化するのが特徴だ。それは引き算 をご存じの皆さんなら分かるだろう。この2変数関数が微分の理解に必要になる。
a-b
小学校で習う速さは、2変数関数
小学校で習う速さは、2変数関数
次に、小学校で登場する「速さ」を考えよう。みはじの公式(海外ではDST triangle)などで覚えたように、「速さ=移動距離÷時間」の割り算は簡単で、小学校でさんざん計算練習し、車のスピードメーターなどでも身近なため、速さという物理量は我々にとって最も身近な概念になっている。落下の速さを定義すると、以下のようになる。
r[t_]:=4.9;(*時刻tにおける落下距離r(t)の関数定義*)v[t_,T_]:=;(*測定開始時刻tから測定時間Tの間の速さvの関数定義。分子のr(t+T)-r(t)が測定中の移動距離になる。*)
2
t
r[t+T]-r[t]
T
このように速さは入力変数が測定開始時刻 と測定時間 の2変数関数になる。 に慣れるため、いくつか例を計算させてみよう。
t
T
v(t,T)
例5:測定開始時刻 t=0s から測定時間 T=0.5s の間の速さ v(0,0.5)の正解を出力させる。
In[]:=
v[0,0.5]
Out[]=
2.45
つまり速さ 2.45 m/s だ。実際、例1、例3から、測定開始時刻 0s と終了時刻 0.5s においてそれぞれ 0m, 1.225m なので、 となる。これと同じ数学演算(代入・四則演算)を Mathematicaが行っているだけだ。
t
t+T
r(0)
r(0.5)
v(t,T)
r(t+T)-r(t)
T
r(0.5)-r(0)
0.5
1.225-0
0.5
2.45
例6:測定開始時刻 t = 0.5 s から測定時間 T = 0.5 s の間の速さ v(0.5, 0.5)の正解を出力させる。
In[]:=
v[0.5,0.5]
Out[]=
7.35
つまり速さ 7.35 m/s だ。例2から測定終了時刻 1sにおける距離 が分かるので手計算も出来る。例5と例6で重要なのは、測定時間 が同じ0.5秒間 でも、測定開始時刻が違うと速さが異なることだ。この依存性は、以下のように変数を残したままで、結果を簡約化する(=簡単にする)コマンドの FullSimplifyを用いることで以下のように求められる。
r(1)
T
t
t
例7:ある測定開始時刻 t から測定時間 T = 0.5 s の間の速さ v(t, 0.5) を、時刻 tを用いて表せ
In[]:=
FullSimplify[v[t,0.5]]
Out[]=
2.45+9.8t
答えは時刻の1次関数の形になる。このように変数を一部残す計算も、Mathematicaのような記号処理ソフトでは可能になる。これが電卓と違う点である。
t
at+b
最後に入力変数の個数にもう一度注目しておこう。もともとの2変数関数に対し、例7のは、変数のみに依存する1変数関数になった。さらに続けて、変数にも定数を代入すると例5のや例6ののように、変数が0個となり、関数の出力値は定数になる。いうなれば、「0変数関数」は定数である。
v(t,T)
v(t,0.5)
t
9.8t+2.45
t
v(0,0.5)
v(0.5,0.5)
小学校の習う速さは、1変数関数ではない!
小学校の習う速さは、1変数関数ではない!
小学校で定義される速さは2変数関数だった。にもかかわらず、我々は気づかぬうちに、「現在の速さ」や「初期時刻の速さ」のような「時刻 の1変数関数の速さ」を理解してしまう。その時、「速さの測定時間はいくつか?」と疑問に思う事さえなく、未定義量を理解してしまう。これが微分の学修の上で、あるいは微分を「楽しむ」上で障害になる。何故なら、定義済みの「2変数関数の速さ 」から、未定義の「1変数関数の速さ」を導く数学演算が17世紀に生み出されており、その演算が今は「微分法」として確立しているからだ。
v(t,T)
t
v(t)
T
v(t)
v(t,T)
r(t+T)-r(t)
T
v(t)
微分とは何か?
微分とは何か?
微分法は「1変数関数の速さ」を導く数学演算になる。先に、機械(Mathematica)に微分させる方法を学び、後から微分法の定義について考えていこう。
v(t)
微分のさせ方
微分のさせ方
問題文で与えられた距離の関数r(t) から、時刻における速さ r’(t)を求める事を「微分する」という。Mathematicaでは定義された関数 r[t] に対し、 ダッシュ(’)をつけてr’[t] とすると微分の正解を出力する。
t
例8:n次関数 を微分すると(t)anになることを、Mathematicaに出力させよ。
r(t)a
n
t
′
r
n-1
t
r[t_]:=a;(*n次関数の定義*)r'[t](*定義された関数r[t]を微分させる*)
n
t
Out[]=
an
-1+n
t
さらに、べき指数を -1+n ではなく、 n-1 にする慣用的な表記は以下のように得られる。
In[]:=
r'[t]//TraditionalForm
Out[]//TraditionalForm=
an
n-1
t
Mathematicaが正解を出力するのは、微分公式を記憶済みだからに過ぎない。具体的に落下公式の を微分するならば、先ほどの式に「当てはめて」、 と、a=4.9を代入し四則演算すればよいが、それさえもMathematicaにまかせればよい。
r(t)4.9
2
t
n2
例9: 落下公式の関数 を微分させよ。
r(t)4.9
2
t
r[t_]:=4.9;(*落下距離の関数の定義*)r'[t](*定義された関数r[t]を微分させる*)
2
t
Out[]=
9.8t
例10:関数 を微分させよ。
r(t)0
In[]:=
r[t_]:=0;r'[t](*定義された関数を微分する*)
Out[]=
0
Mathematicaだけではなく、多くの高校生にとって微分の計算は、まるで掛け算の九九のように、丸暗記した表をもとに、問題に当てはめていくだけの作業である。
微分の演算方法の初歩
微分の演算方法の初歩
機械に微分させる方法が分かった所で、いよいよ「2変数関数の速さ 」から「1変数関数の速さ」を定義しよう。
v(t,T)
v(t)
静止の速さ~ルール1簡約化~
静止の速さ~ルール1簡約化~
1変数関数の速さ は未定義なのだが、皆さんは「静止している時刻における速さはゼロ」にしたいと思わないだろうか。別の問い方をするなら、あなたが人類で初めて、速さ を定義するとしたら、「静止なら速さゼロ」になるように定義するのではないか?このあなたの欲求、あるいは人類のニーズを満たす数学演算が微分法の初歩になる。
v(t)
t
v(t)
v(t)
「静止」も「速さ」も身近な概念なので、それを用いて我々も、微分法という数学演算を「作る」ことが出来る。まず、落下の公式を離れて、「静止」を考えよう。例えば、いつでも、つまり「どんな時刻 でも」、落下距離0mになる物体は、(空中に)静止しているだろう。これは と表現される。
t
r(t)0
静止を意味する に対し、速さを計算すると、のみ「場合分け」が必要で、 =不定, となる。実際、測定時間の場合には、以下のエラーが発生し、出力として Indeterminate (不定)を出す。
r(t)0
v(t,T)
r(t+T)-r(t)
T
T0
v(t,T)0,(T≠0)
0-0
T
0
T
v(t,0)
0
0
(T0)
T0
In[]:=
r[t_]:=0(*どんなtでもr=0となる関数を定義*)v[t_,T_]:=;v[t,0](*測定時間T=0の速さ*)
r[t+T]-r[t]
T
1
0
Out[]=
Indeterminate
結局、我々のニーズ(静止の速さゼロ)を満たすには、単に「測定時間はゼロ時間ではない()」というルールを作ればよいと分かる。このルールは、微分法でも非常に重要になる。Mathematica では、ルールを満たすコマンドはFullSimplify で、これは内部でとして 0と置き換える。よって以下のように1変数関数 v[t] を「定義」できる。
T≠0
T≠0
0
T
v[t_]:=FullSimplify[v[t,T]];(*簡約化FullSimplifyでは0/T=0として、不定を回避できる*)
これが、微分法の第一歩になる。実際、以下のように我々のニーズ(静止の速さゼロ)を満たし、かつ微分法の正解と一致する。
r[t_]:=0;(*どんな時刻tでも落下距離はr=0で、静止している*)v[t](*定義された関数r(t)に対し、時刻tにおける速さv(t)を出力*)
よって、微分法の正解(例10)と一致する。
後編「ルール2:置換代入」へ…
後編「ルール2:置換代入」へ…
ここまでで、静止というシンプルなケースを出発点に、微分法の第一歩となる「ルール1:簡約化」を学びました。しかし、物体が落下する場合には、速さを求める計算に測定時間Tが残り、実は1変数関数にはなりません。
この問題をどう解決するのか――それが次のステップ、ルール2:置換代入です。
続きは後編で解説します。
ここまでで、静止というシンプルなケースを出発点に、微分法の第一歩となる「ルール1:簡約化」を学びました。しかし、物体が落下する場合には、速さを求める計算に測定時間Tが残り、実は1変数関数にはなりません。
この問題をどう解決するのか――それが次のステップ、ルール2:置換代入です。
続きは後編で解説します。