The Integraph: An Integrating Mechanism
The Integraph: An Integrating Mechanism
Before the Differential Analyzer and long before Mathematica or Wolfram|Alpha, mechanical instruments were used to perform computations. The "Integraph"[1] in this Demonstration plots the integral curve starting from a given curve .
F(x)
f(x)
This mechanism was first designed by Bruno Abakanowicz[2] and further perfected by Gottlieb Coradi[3] in Zurich around 1905 using a carriage in the shape of a parallelogram. These instruments are similar, in principle, to the planimeter, a device that can measure the area inside a closed curve.
According to the manufacturer: "By means of the integraph many of the most difficult calculations and problems occurring in the practice of an engineer in shipbuilding, bridge and iron constructions, earth transports, electronics, technical optics and ballistics can be solved in a simple and reliable manner with much saving of time and the operator need not possess any knowledge of higher mathematics."[4].
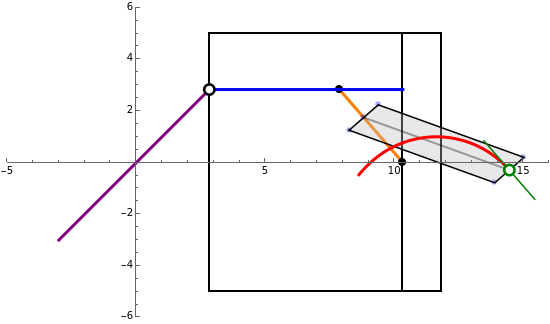
Move the input pen along the curve for the function to generate the integral curve.
f(x)
Details
Details
The integral curve is drawn by a pen that moves in a (tangential) direction proportional to the local value of the given curve. This is achieved by the following mechanism.
The integraph consists of a rectangular carriage that moves left to right on rollers along the axis.
x
Drag the input pen along the given curve, following a given path . The input pen moves a trolley up and down the carriage and rotates the main arm around a fixed point on the carriage. The direction of the main arm is a function of the input .
f(x)
ϕ(x)
f(x)
ϕ(x)=-
-1
tan
f(x)
2
L
2
f[x]
L
The output pen is guided parallel to the main arm by means of a tangential wheel connected to the main arm by a parallelogram linkage. This way the tangent of the output curve will be proportional to the input . This is expressed by the differential equation
F'(x)
F(x)
f(x)
F'(x)tanϕ(x)
with solution .The parallelogram keeps the wheel parallel to the main arm, independent of the vertical position of the output pen.
F(x)=-dx
f(x)
2
L
2
f(x)
References
References
[4] P. Garcia. "Integraphs," DrawingMachines.org. (Dec 4, 2015) drawingmachines.org/category.php?id=36.
Permanent Citation
Permanent Citation
Erik Mahieu
"The Integraph: An Integrating Mechanism"
http://demonstrations.wolfram.com/TheIntegraphAnIntegratingMechanism/
Wolfram Demonstrations Project
Published: December 7, 2015