
You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
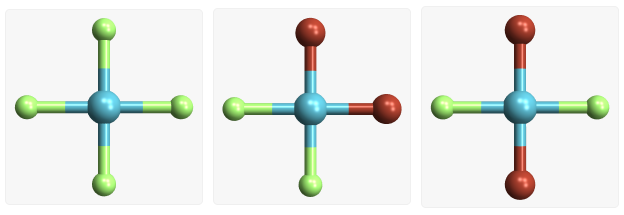
Square planar molecules |
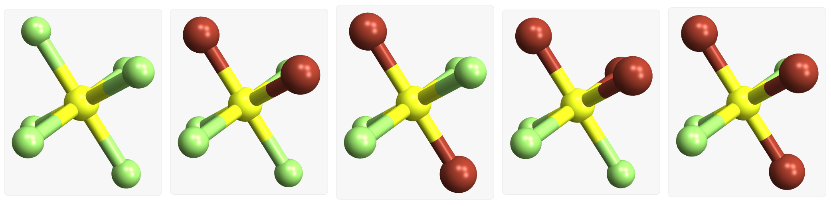
Octahedral molecules |
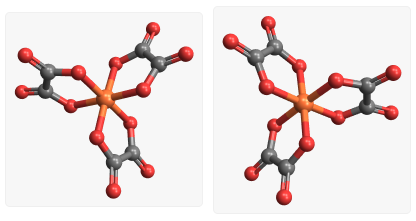
Optical isomers |
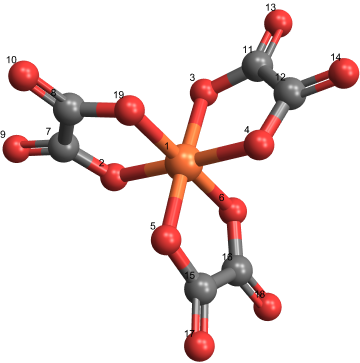
Lambda molecule |
Graphics[ |
Graphics[ |
Graphics[ |
Graphics[ |
Graphics[ |
Graphics[ |

You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »