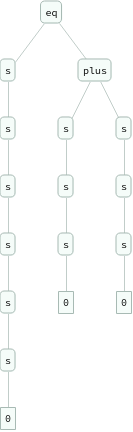
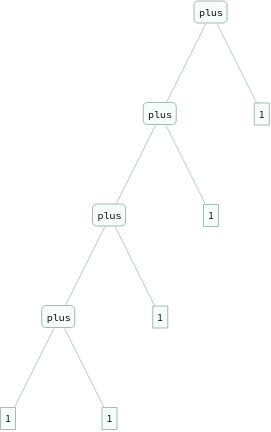
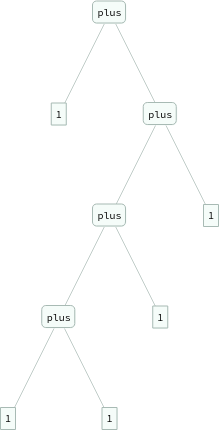
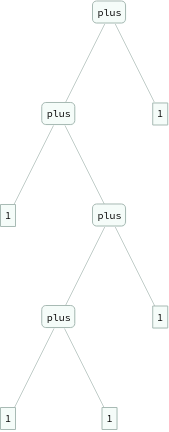
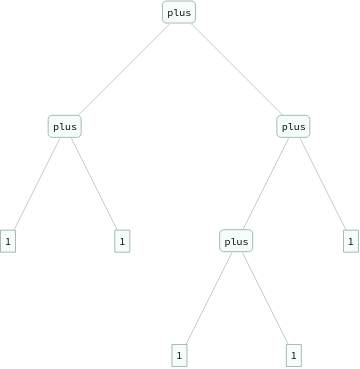
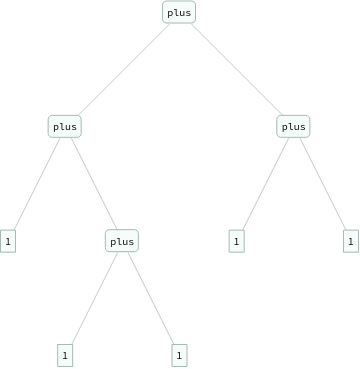
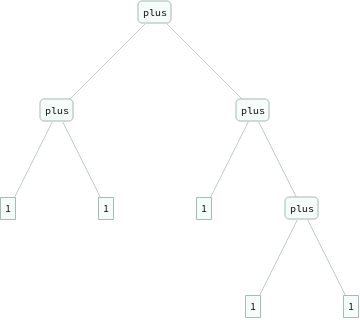
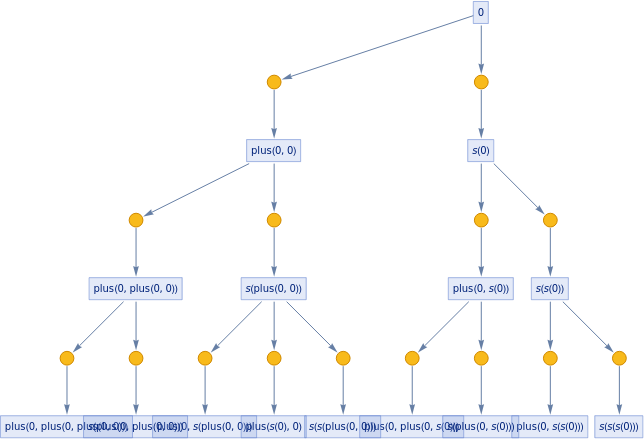
In[]:=
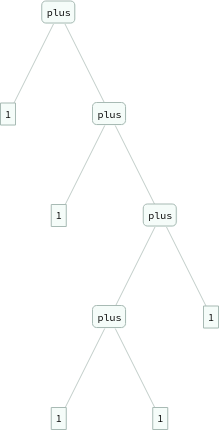
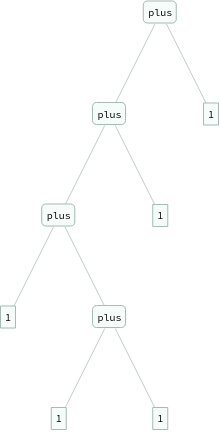
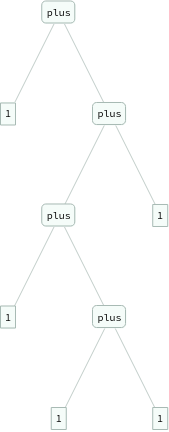
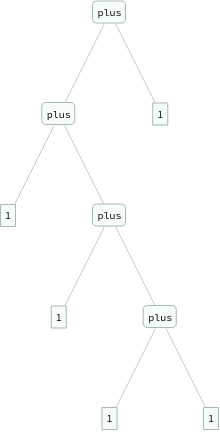
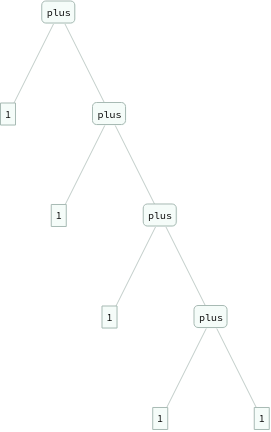
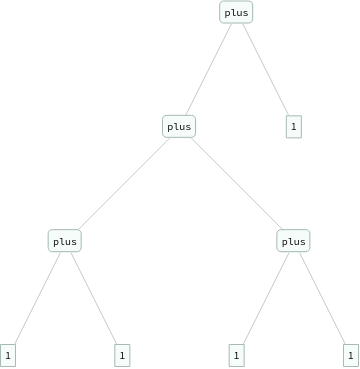
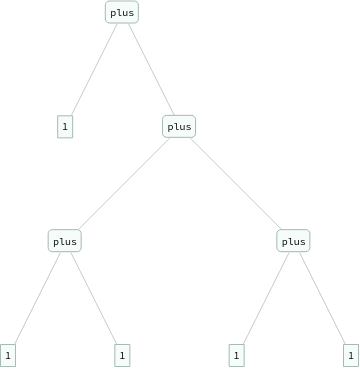
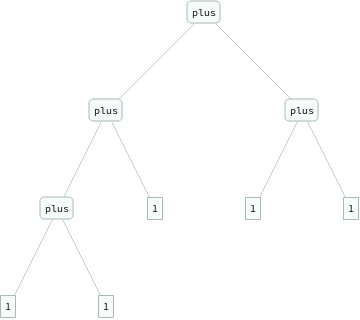
ExpressionTree/@Flatten[Table[eq[Nest[s,0,i+j],plus[Nest[s,0,i],Nest[s,0,j]]],{i,3},{j,3}]]
Out[]=

,
,
,
,
,
,
,
,

{eq[a_,b_],eq[b_,c_]}->{eq[a,c]}

What are the rules for combining these results?

In[]:=
ExpressionTree/@Groupings[{1,1,1,1,1},plus->2]
Out[]=

,
,
,
,
,
,
,
,
,
,
,
,
,


Rules for equivalence relations...

equal[a_,b_]->equal[b,a]
{eq[a_,b_],eq[b_,c_]}->{eq[a,c]}
plus[0,a_]->a
plus[s[a_],b_]->s[plus[a,b]]
In[]:=
plus[Nest[s,0,3],Nest[s,0,2]]
Out[]=
plus[s[s[s[0]]],s[s[0]]]
In[]:=
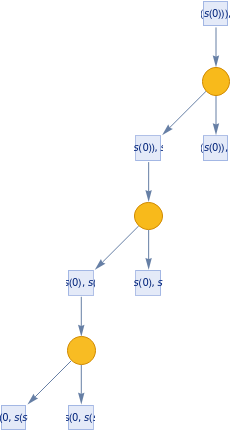
TokenEventGraph[{{plus[s[a_],b_]}:>{s[plus[a,b]]},{plus[0,a_]}:>{a}},{plus[Nest[s,0,3],Nest[s,0,2]]},3]
Out[]=
In[]:=
TokenEventGraph[{{plus[s[a_],b_]}:>{s[plus[a,b]],plus[a,b]},{plus[0,a_]}:>{a}},{plus[Nest[s,0,3],Nest[s,0,2]]},3]
Out[]=
Needs treelike replacements...
In[]:=
Replace[plus[Nest[s,0,3],Nest[s,0,2]],plus[s[a_],b_]:>s[plus[a,b]]]
Out[]=
s[plus[s[s[0]],s[s[0]]]]

Two kinds of “equality”: (1) “symbolic equality”, (2) substitutional equality

equal[a,a]
In[]:=
TokenEventGraph[{{a_}:>{s[a]},{s[plus[a_,b_]]}:>{plus[s[a],b]},{a_}:>{plus[0,a]}},{0},3]
Out[]=

Can we construct “true theorems” (i.e. equalities) of the Plus world?

In Polish notation, we have to have strings-as-linked-lists to thread things back together

Or use trees, then have reinsertion...

Can have rules that apply themselves at any level.... (cf https://www.wolframcloud.com/obj/wolframphysics/Tools/combinators )

This is only establishing True for a particular

Multicomputational evaluator

Ordinary case:
Transformations get done by mapping through the expression, and by reevaluation....
The usual evaluator involves a single total ordering of updates....
[ Rules can’t have been assigned because then the ordinary evaluator will try to use them ]

Things one could compute

◼
  • Set of normal forms (e.g. multibranch recursive function)
    • ◼
  • Path weight to normal form
    • ◼
  • Existence of path to a given expression
    • ◼
  • Path to a given expression, with all “incoming tentacles” included [i.e. proof of path]
    • ◼
  • Equivalence classes of expressions produced
    • ◼
  • Collections of expressions that can be considered “complete states”

    • Issue: whether to include path weights or not [included if there is not deduplication]

    Note: could look not for normal form, but for repeating form, etc. [and could do this in the ordinary evaluator as well]

    Loop detection in the ordinary evaluator

    What “trivial” behavior can occur?

    Once it’s trivial, it’s pretty much guaranteed not to terminate....

    Tree walking in the multicomputation graph

    Can put events in a certain order based on where they occur on the tree... The foliation corresponds to the traversal order...

    Want to number nodes to indicate traversal order

    Cross-Reference of Theorems

    This is a token-event graph sampled only for the “humanly interesting theorems”

    Coarse-graining is by human aesthetics

    Type Theory?

    Homotopy type theory

    Univalence axiom : “equivalence is equivalent to equality”
    [[ Patterns are equivalent to types ... ]]

    Type being inhabited ⇔ set has an element ⇔ [there is a construction for things of that type]

    List : product type ; Alternatives : sum type
    Except[_] : void type
    Proof of inhabitance: exhibit an expression that matches

    Analogous statement? paths with the same

    Tokens vs events :: expressions vs transformations

    Mathematics

    Translation between mathematical axiom systems ⇔ time dilation

    Singularities ⇔ decidability

    Proof density ~ energy

    Different axiom systems ⇔ reference frames

    wrt a universal collection of proofs defined by a certain law of inference

    Geometer vs algebraist: different reference frames + different coarse graining

    At “mathematician scale” many equivalences are used: e.g. there are [700] underlying representations of a pentagon, but the mathematician says it’s a pentagon

    Is there a universal mathematician? Category theorist

    Continuum hypothesis:

    1. It’s a certain reference frame that makes it true or false
    2. There’s no human-compatible reference frame that makes it false (cf naked singularities ; no computable reference frame)

    Event horizon: separated area of math that’s decidable

    E.g. you can’t derive number theory from Boolean algebra

    Can there be a cosmological event horizon: math is broken into two parts?

    Is the mathematical universe expanding? Yes, at the level of tokens. Not so obvious at the coarse-grained level

    Limit of mathematics: it’s all connected, except for the black holes [decidable theories] ... but note that there might be “no hair” for decidable theories ... i.e. they are all the same

    What is the distribution of mathematical statements in “mathematical branchial space”?

    Is there an analog of physical space in mathematics, or is it all branchial? [Is there an analog of pure motion in math?]

    Feature of ruliad: physical and branchial space are somehow equivalent

    What is the quantum theory of mathematics?

    It’s associated with the story of multiple proofs ;
    right now, math is classical, because you just want to know that there is a proof...
    Does the mathematical observer conflate proofs?
    [“Extensional equality” : conflate all proofs]
    [“Intensional equality” : multiple proofs construct the same result ]
    < QM is about stopping part way through the proof, and seeing the distribution of where you got >
    [ How do you parametrize the threads of proof? ]
    Destructive interference: two proofs that have very distant intermediate stages [i.e. no single mathematician can “hold those two proofs in mind at the same time” (or they are actually contradictory) [ in terms of patterns, it becomes patterns that can’t be unified ] [ destructive interference: you have to prove the conjunction of the intermediate statements ]
    [ probability distributions on intermediate proof states ]

    [[ Virtual particles: ~ p⋁¬p continually being generated ]]

    [ ?? path integral in math ]

    Are TEGs (“multicomputational graphs”) a good machine code for all foundational idealizations of math?

    Equational proofs
    Modus ponens proofs
    HTT
    Intuitionism

    ⟶ metametamathematics

    WL is meta computational mathematics [general description of computational math]
    WL is not (yet) the general description of proof-based math [needs a new evaluator]

    What is a particle in math?

    Related to persistent concepts that exist at the “observer level”

    Reference frame is defined by a set of patterns

    Particle is a persistently matching expression that continues at different slices in the foliation

    Foundations of computational math vs. foundations of mathematicians’ mathematics

    In a sense, Hilbert already defined the machine code of math ; like we’ve defined machine code of physics
    But he didn’t figure out the continuum limit

    Metamathematical space is the space in which the continuum limit will play out...