Ammonia Inversion: Classical and Quantum Models
Ammonia Inversion: Classical and Quantum Models
The ammonia molecule has a trigonal pyramidal configuration, with the nitrogen atom connected to three hydrogen atoms. The molecule readily undergoes inversion at room temperature, like an umbrella turning itself inside out in a strong wind. The energy barrier to this inversion is 24.2 kJ/mol. A resonance frequency of 24.87 GHz, in the microwave region, corresponds to the energy splitting of the two lowest vibrational levels. This transition is exploited in the ammonia maser.
NH
3
In quantum mechanics, ammonia inversion can be described by a simplified Schrödinger equation
-''(x)+V(x)(x)=(x)
1
2μ
ψ
n
ψ
n
E
n
ψ
n
where is the axial position of the nitrogen atom. The appropriate reduced mass is given by
x
μ=+3
3
m
N
m
H
m
N
m
H
We consider a model for the potential energy of the form
V(x)==-+
2
k(-)
2
x
2
r
8
2
r
k
2
r
8
k
2
x
4
k
4
x
8
2
r
where is the N-H bond distance. The value at gives the inversion barrier =.
r
x=0
V
0
k
2
r
8
Since the Hamiltonian contains only even powers of and , a representation based on the ladder operators and suggests itself, a generalization of the canonical operator formulation for the harmonic oscillator.
p
x
a
†
a
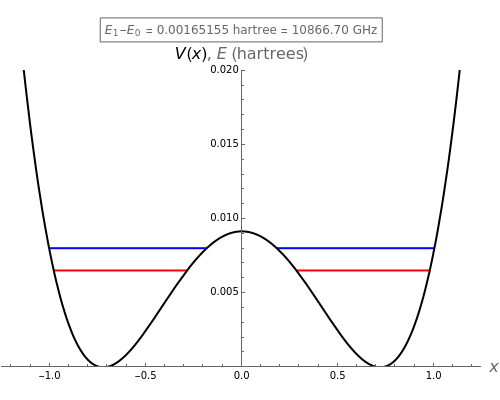
The computation results in a secular equation for the eigenvalues, which are plotted on the graph superposed on the potential energy curve. The blue and red lines correspond to eigenstates that are, respectively, symmetric and antisymmetric with respect to inversion. The eigenvalues tend to occur in closely spaced pairs, with the - splitting representing the transition in the ammonia maser. The optimal choice of adjustable parameters is shown by clicking "optimize".
E
1
E
0
Details
Details
The ladder operators can be defined by
a=x+ip
μω
2
1
2μω
†
a
μω
2
1
2μω
with an adjustable parameter introduced. The nonvanishing matrix elements of the Hamiltonian can then be computed, giving
ω
H
n,n
1
32
(6+6n+3)k
2
n
2
r
2
μ
2
ω
2
r
(8n+4)k
μω
H
n+2,n
H
n,n+2
(n+1)(n+2)
-4+(2n+3-2μω)k
2
r
2
μ
3
ω
2
r
16
2
r
2
μ
2
ω
H
n+4,n
H
n,n+4
(n+1)(n+2)(n+3)(n+4)
k32
2
r
2
μ
2
ω
The eigenvalues are then determined using the Eigenvalue routine for selected dimensions 2 to 10.
References
References
[1] S. M. Blinder, "Ammonia Inversion Energy Levels Using Operator Algebra." arxiv.org/abs/1809.08178.
Permanent Citation
Permanent Citation
S. M. Blinder
"Ammonia Inversion: Classical and Quantum Models"
http://demonstrations.wolfram.com/AmmoniaInversionClassicalAndQuantumModels/
Wolfram Demonstrations Project
Published: February 22, 2019