Trisection by Sliding a Line

angle AOB (α)

move D

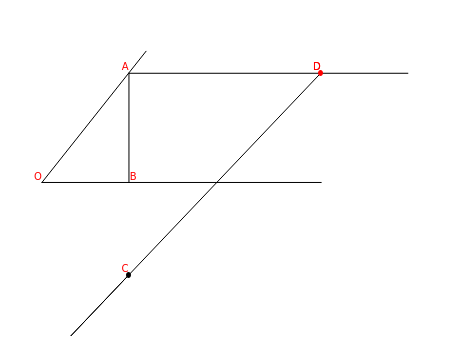
This Demonstration shows how to trisect an angle by sliding a line. Adjust the angle to trisect,

AOB

, and then move point

D

so that the point

O

is on the line

CD

. The point

C

is chosen so that

CD

is twice

OA

. The angle

COB

is a third of the angle

AOB

.

Details

Let

α=∠BOA

. Assume the line

AD

is parallel to

OB

,

AB

is perpendicular to

OB

, and

CD=2OA

. If the point

O

is on the line

DC

, and

CE=ED=OA

, then triangles

OEA

and

AED

are isosceles. The angles

EAD

and

EDA

are equal and are equal to

BOC

, but their sum equals

AEC=COA

. So

2α=2∠BOC=∠COA

.

The problem goes back to ancient Greece, with contributions by Hippocrates, Archimedes, and Pappus.

References

[1] P. Berloquin, The Garden of the Sphinx, New York: Scribner's, 1985 p. 179.

[2] J. J. O'Connor and E. F. Robertson. "Trisecting an Angle." (Jun 21, 2012) www-history.mcs.st-and.ac.uk/HistTopics/Trisecting_an_angle.html.

External Links

Archimedes's Neusis Angle-Trisection

Kempe's Angle Trisector

Yates's Trisector

Permanent Citation

Izidor Hafner

"Trisection by Sliding a Line"
http://demonstrations.wolfram.com/TrisectionBySlidingALine/
Wolfram Demonstrations Project
Published: July 3, 2012