Simple Reaction with Segregation in a Batch Reactor

initial concentration ratio

A

0

/

B

0

0.5

Damköhler number

5

Consider a simple chemical reaction

A+B→C

in a batch reactor. The reaction rate in terms of the intensity of mixing,

I

, is given by:

-

r

A

=-

c

A

c

B

=-k

-

c

A

-

c

B

-I

-

c

A0

-

c

B0



, where

c

A

and

c

B

are the instantaneous concentrations,

-

c

A

and

-

c

B

are the mean concentrations, and

-

c

A0

and

-

c

B0

are the initial concentrations of species

A

and

B

. The governing equation is the following:

d(

-

c

A

)

dt

=

-

r

A

.

This equation can be written in dimensionless form as:

dy

dθ

=-

D

a

(y(y+η-1)-Iη)

, where

η=

-

c

B0

-

c

A0

is the initial concentration ratio,

θ=

t

τ

m

is the dimensionless time,

τ

m

is the mixing time,

y=

-

c

A

-

c

A0

is the dimensionless concentration,

D

a

=k

-

c

A0

τ

m

is the Damköhler number (a dimensionless number that is a measure of the reaction time versus mixing time), and

I=

-

t

τ

m

e

is the degree of segregation.

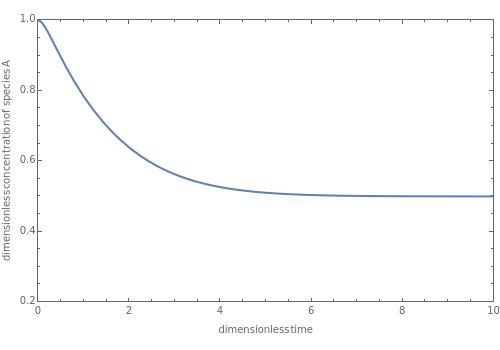
This Demonstration displays the dimensionless concentration versus the dimensionless time for various values of the Damköhler number and the initial concentration ratio. It is straightforward to see that the steady-state dimensionless concentration is independent of the Damköhler number. The Damköhler number has an influence only on how fast this steady-state dimensionless concentration is reached. This steady-state dimensionless concentration is equal to

y

ss

=1-η.

When

D

a

→∞

, there is an analytical expression for the dimensionless concentration, which is given by:

y

∞

(θ)=

-(η-1)+

2

(η-1)

+4ηI

2

, with

I=

-θ

e

.