Limaçons as Envelopes of Circles

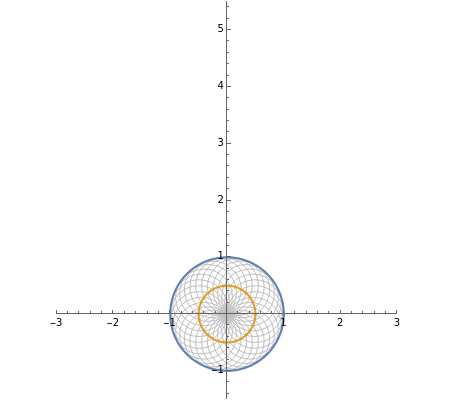
A limaçon can be defined as the envelope of the circles that pass through a fixed point P and have centers on a given circle

C

. In this Demonstration, P is the origin. You can vary the center of the circle

C

(shown in red) to see the envelope (shown in blue) change. Unchecking the "show limaçon" checkbox lets you picture the envelope on your own.

Snapshot 1: when P is at center of the circle

C

, the envelope is a circle

Snapshot 2: when P is in the interior of

C

but not at its center, the envelope is a dimpled limaçon

Snapshot 3: when P is on

C

, the envelope is a cardioid

Snapshot 4: when P is outside of

C

, the envelope is a limaçon with an interior loop

Daniel Joseph