Double Delta Function Scattering Potential
Double Delta Function Scattering Potential
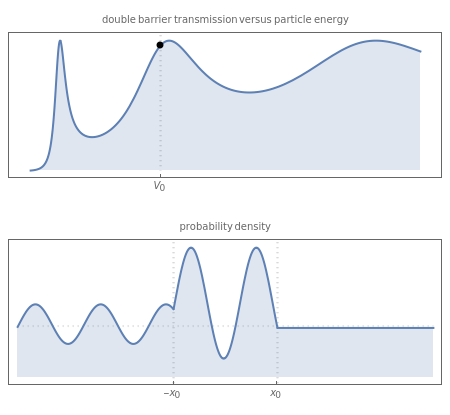
This Demonstration illustrates the transmission of a quantum-mechanical particle through a double delta function potential in one dimension. Multiple scattering between the two delta functions gives rise to resonances that depend on the spacing between the two delta functions as well as on the energy of the scattering particle.
Details
Details
The one-dimensional double delta function potential, , is perhaps the simplest example of a scattering problem exhibiting the phenomenon of resonance. As the scattering wavefunctions can be found in closed form, it constitutes a very useful textbook-style example.
V(x)=(δ(x-)+δ(x+))
V
0
x
0
x
0
The resonance can be thought of as arising from interference between paths that are reflected a different number of times between the two barriers. In this Demonstration, both the energy of the incoming particle and the spacing between the two barriers can be varied.
Snapshot 1: lowest order resonance, corresponding to approximately half a wavelength between the two barriers
Snapshot 2: increasing the separation between the barriers decreases the energy of resonant transmission: here is the third resonance for a wider double barrier
Snapshot 3: bringing the barriers together destroys the resonance effect: here the barriers are very close together and the transmission function is very close to that of a single barrier
External Links
External Links
Permanent Citation
Permanent Citation
Peter Falloon
"Double Delta Function Scattering Potential"
http://demonstrations.wolfram.com/DoubleDeltaFunctionScatteringPotential/
Wolfram Demonstrations Project
Published: March 7, 2011