Computational: a rule gives a successor for each state
Computational: a rule gives a successor for each state
Multicomputational: a rule relates multiple states
Multicomputational: a rule relates multiple states
One state is transformed into several; several states are used to determine one new state
In FindEquationalProof, one combines two theorems to get another one.... [inference rule] (“superposition”)
(“left superposition” vs. “right superposition”)
(“left superposition” vs. “right superposition”)
“Critical pair lemmas are generated by completions, superpositions, and paramodulations”
“Substitution lemmas are generated by resolutions and factorings”
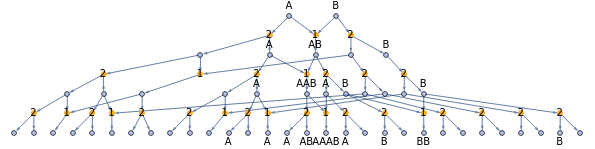
String-based 21
String-based 21
StringJoin
In[]:=
MIMWGraph[{{n_,m_}:>{StringJoin[n,m]}},{"A","B"},3,UniqueTokens->True,Overlaps->False,VertexLabeling->True]
Out[]=
In[]:=
MIMWGraph[{{n_,m_}:>{StringJoin[n,m]}},{"A","B"},3,UniqueTokens->True,Overlaps->True,VertexLabeling->True]
Out[]=
In[]:=
MIMWGraph[{{n_,m_}:>Flatten@{StringJoin[n,m],StringTakeDrop[n,UpTo[1]]}},{"A","B"},3,UniqueTokens->True,Overlaps->False,VertexLabeling->True]
Out[]=
In[]:=
MIMWGraph[{{n_,m_}:>{StringJoin[n,m]},{n_}:>StringTakeDrop[n,UpTo[1]]},{"A","B"},3,UniqueTokens->True,Overlaps->False,VertexLabeling->True]
Out[]=
In[]:=
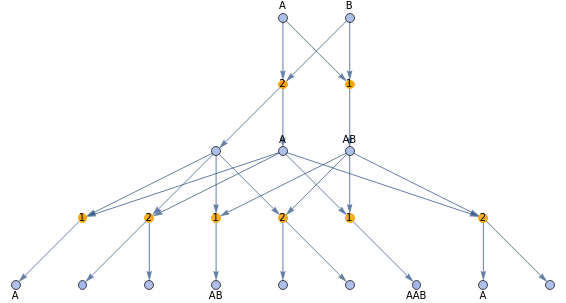
MIMWGraph[{{n_,m_}:>{StringJoin[n,m]},{n_}:>StringTakeDrop[n,UpTo[1]]},{"A","B"},2,UniqueTokens->True,Overlaps->False,VertexLabeling->True]
Out[]=
In[]:=
MIMWGraph[{{n_,m_}:>{StringJoin[n,m]},{n_,m_}:>StringTakeDrop[n,UpTo[1]]},{"A","B"},2,UniqueTokens->True,Overlaps->True,VertexLabeling->True]
Out[]=
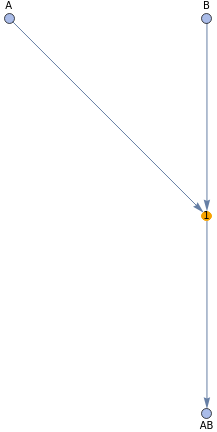
Spacelike-separated events: one token, multiple events
Spacelike-separated events: one token, multiple events
I.e. several things can happen to one token
The most recent common ancestor is a token
The most recent common ancestor is a token
Branchlike-separated events: one event can lead to multiple histories
Branchlike-separated events: one event can lead to multiple histories
The most recent common ancestor is an event
In the WM case, each token is a hyperedge .... but there are other “identities” between hyperedges not captured by the evolution
In the WM case, each token is a hyperedge .... but there are other “identities” between hyperedges not captured by the evolution
Fully deduplicated:
Fully deduplicated:
Petri net analogy: Expressions are places; events are transitions
As soon as there is branchlike or spacelike separation of events, there is ambiguity
As soon as there is branchlike or spacelike separation of events, there is ambiguity
But with causal invariance, there is ultimately no ambiguity in the causal graph
But with causal invariance, there is ultimately no ambiguity in the causal graph
[ I.e. there is invariance in the causal graph, independent of the reference frame / evaluation order ]
Is category theory capturing the inexorable structure?
Is category theory capturing the inexorable structure?
A causal graph is only nontrivial if the full multihistory is a nontrivial multiway graph
A causal graph is only nontrivial if the full multihistory is a nontrivial multiway graph
Sequential always does only one update at a time ... even though multiple can be done....
Where does inexorable structure come from?
Where does inexorable structure come from?
E.g. for CA, there is an inexorable light cone...
Can there be a multiway system in which there is no notion of space?
Can there be a multiway system in which there is no notion of space?
E.g. numerical multiway systems
A foliation of this says which numbers can appear “at the same time”
Is the causal graph the same as the multiway graph in this case? [And there seems to be no space; only branchlike separation]
To find places where different foliations are possible, look for branch pairs
This isn’t a valid foliation:
What antichains exist here? These are the possible foliations...
What antichains exist here? These are the possible foliations...
Existence of multiple reference frames forces a certain continuity.... (?)
Existence of multiple reference frames forces a certain continuity.... (?)
Continuity must come from small variations of the foliation .... within the family of foliations......
Computational irreducibility + computational boundedness
Computational irreducibility + computational boundedness