Transformations of Complex, Dual, and Hyperbolic Numbers

type

complex

dual

hyperbolic

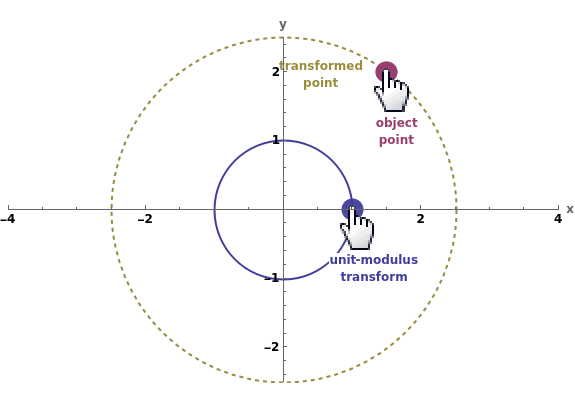
This Demonstration compares the multiplicative transformation properties on the

x,y

plane of complex, dual, and hyperbolic numbers. These number types share the form

z=x+βy

, where

and

are real numbers and

has the defining characteristics:

=-1

for complex numbers,

for dual numbers, and

=+1

for hyperbolic numbers. Their conjugates share the form

=x-βy

and their modulus the form

The figure shows, for the selected number type,

1. a transform point on its unit-modulus locus (in blue),

2. an object point in the plane (in red), and

3. the point resulting from their multiplicative transform on its trajectory (in brown).

In the complex plane, multiplying by a unit-modulus transform produces a rotation about the origin; in the dual plane, it produces a translation in the pure dual direction, and in the hyperbolic plane, a traversal of an hyperbola that passes through the object point.

Details

Hyperbolic numbers (sometimes called split-complex numbers) are useful for measuring distances in the Lorentz space-time plane (see G. Sobczyk, "The Hyperbolic Number Plane," The College Mathematics Journal, 26(4), 1995 pp. 268–280).

External Links

Complex Number (Wolfram MathWorld)

Dual Number (Wolfram MathWorld)

Iterated Maps Using Complex, Dual, and Split-Complex Numbers

Permanent Citation

Fred Klingener

"Transformations of Complex, Dual, and Hyperbolic Numbers"
http://demonstrations.wolfram.com/TransformationsOfComplexDualAndHyperbolicNumbers/
Wolfram Demonstrations Project
Published: March 7, 2011