The Log Normal Distribution

parameter μ

0.

parameter σ

1.

mean:	μ+ 2 σ 2 	=	1.649
variance:	2μ+ 2 σ  -1+ 2 σ  	=	4.671

If

X

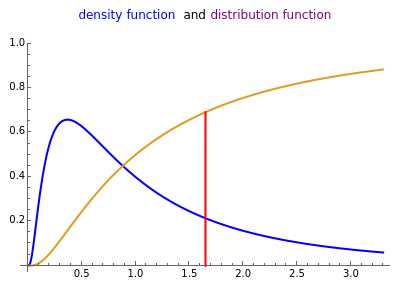
is a normal random variable with parameters

μ

and

σ

, then

Y=

X



is a log normal random variable with the same parameters. Note that

μ

and

σ

are not the mean and standard deviation of

Y

. Just as (by the central limit theorem) the sum of a large number of independent, identically distributed random variables is nearly normal, the product of a large number of independent, identically distributed random variables is nearly log normal. The red vertical line marks the mean of the distribution.

External Links

Log Normal Distribution (Wolfram MathWorld)

Permanent Citation

Chris Boucher

"The Log Normal Distribution"
http://demonstrations.wolfram.com/TheLogNormalDistribution/
Wolfram Demonstrations Project
Published: October 16, 2007