Remainder Graphs
Remainder Graphs
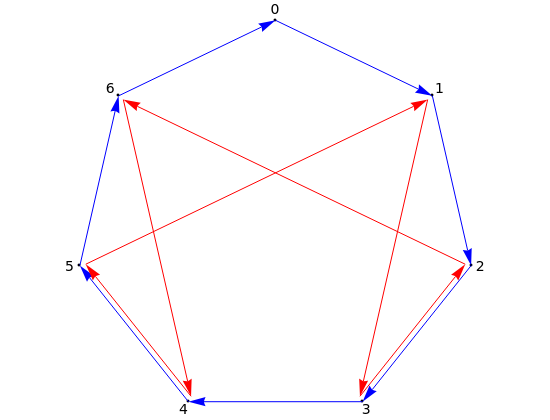
What is the remainder when some number is divided by another number, for example, 7? The result is called . You can find the answer quickly with the help of one of the graphs in this Demonstration.
n
n(mod7)
For a number, say , select the desired modulus, then start at 0 and follow 9 blue arrows, 1 red arrow, 4 blue arrows, 1 red arrow, 0 blue arrows, 1 red arrow, then 6 blue arrows. If there is no red arrow, stay in place. Each digit specifies the number of blue arrows, then follow a single red arrow before moving on to the next digit. The number on your final landing place gives the remainder. In this example, .
n=9406
9406=5(mod7)
References
References
[1] D. Wilson, "Divisibility by 7 Is a Walk on a Graph," Tanya Khovanova's Math Blog (blog, T. Khovanova, owner), (Aug 11, 2009) blog.tanyakhovanova.com/2009/08/divisibility-by-7-is-a-walk-on-a-graph-by-david-wilson.
External Links
External Links
Permanent Citation
Permanent Citation
Ed Pegg Jr
"Remainder Graphs"
http://demonstrations.wolfram.com/RemainderGraphs/
Wolfram Demonstrations Project
Published: November 16, 2015