Tracing a Peritrochoid

​
r: base circle radius = 1​R: rolling circle radius
1.6
d: distance of tracing point to the centerof the rolling circle
1.25
ϕ: rotate the rolling circle
6.
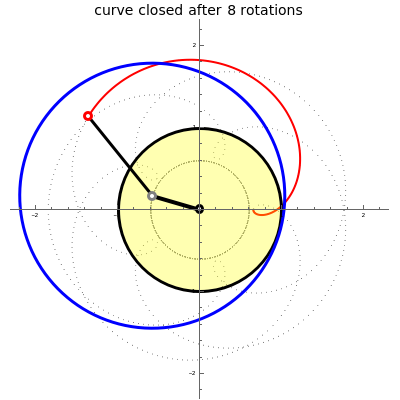
This Demonstration shows a mechanism drawing a peritrochoid.
Like the epitrochoid, a peritrochoid is the roulette traced by a point attached to a circle rolling without slipping around a base circle.
An epitrochoid is formed when the rolling circle is outside the base circle. A peritrochoid is formed when the base circle is inside the rolling circle.
While the traced epitrochoid and peritrochoid are similar, they are generated in different ways.
Peritrochoid curves appear in the kinematics of the Wankel engine[1].

Details

The radius of the stationary circle
r
is set to
1
, and
R
is the radius of the rolling circle.
A peritrochoid is a sum of two rotations of the rolling circle, expressed in terms of their angle vectors:
1. A rotation around the axes origin:
(R-r){cosϕ,sinϕ}
.
2. A rotation around its center:
dcos
(R-r)ϕ
R
,sin
(R-r)ϕ
R

.
The peritrochoid becomes a closed curve after
nR
rotations of the rolling circle, where
n
is the denominator of a rational close to
R
.

References

[1] V. I. Koutsovoulos. "Peritrochoid Curve & the Wankel Engine." Mechanical Drafting Services (Mar 6, 2017) mechdrafting.net/en/portfolio-item/peritrochoid-curve.

External Links

Roulette (Wolfram MathWorld)
Epitrochoid (Wolfram MathWorld)

Permanent Citation

Erik Mahieu
​
​"Tracing a Peritrochoid"​
​http://demonstrations.wolfram.com/TracingAPeritrochoid/​
​Wolfram Demonstrations Project​
​Published: March 7, 2017