Particle in a Box: Probability Density and Positional Variance
Particle in a Box: Probability Density and Positional Variance
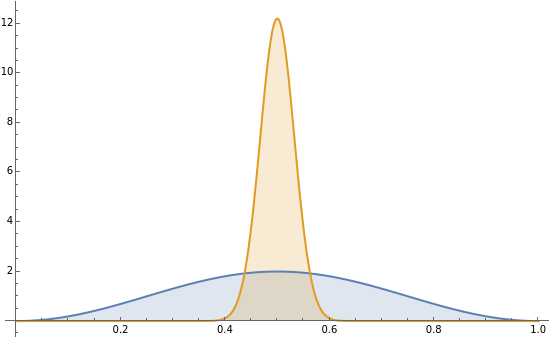
The square of the absolute value of the Schrödinger wavefunction equals the probability density of finding a particle at any point in a box. It is relatively straightforward to show that for all values of , the average or expectation value of the position of the particle will be at the exact midpoint of the box (, where is the length of the box)[1]. The variance, however, increases with increasing quantum number, to a limiting value of /12. This Demonstration plots the probability density (in blue) and a normal distribution (in yellow) with mean and variance 1- to represent the change in the variance with increasing .
n
a/2
a
2
a
a
2
2
a
12
6
2
n
2
π
n
Details
Details
The variance is =-, where the expectation values and are obtained from p(x)dx and xp(x)dx, respectively, where is the length of the box. The (normalized) probability function for the one-dimensional particle in a box is given by[1]:
2
σ
2
x
2
〈x〉
2
x
〈x〉
a
∫
0
2
x
a
∫
0
a
p(x)=
2
a
2
sin
nπx
a
References
References
[1] D. A. McQuarrie and J. D. Simon, Physical Chemistry: A Molecular Approach, Sausalito, CA: University Science Books, 1997.
External Links
External Links
Permanent Citation
Permanent Citation
Daniel Barr
"Particle in a Box: Probability Density and Positional Variance"
http://demonstrations.wolfram.com/ParticleInABoxProbabilityDensityAndPositionalVariance/
Wolfram Demonstrations Project
Published: September 23, 2020