Minimal Enclosing Circle
Minimal Enclosing Circle
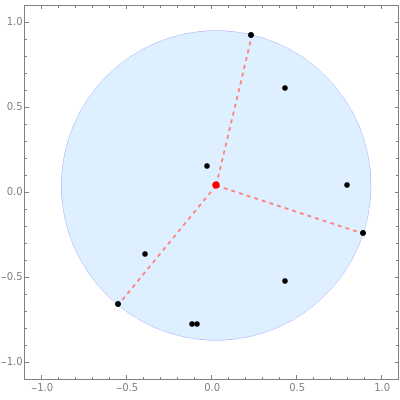
The minimal enclosing circle is the smallest circle that completely contains a set of points. Formally, given a set of points in the plane, find the circle of smallest radius such that all points in are contained in the interior or boundary of .
S
n
C
S
C
Details
Details
Snapshot 1: state the problem with a set of random points in the plane
n
Snapshot 2: find the minimal enclosing circle with two points on its boundary
Snapshot 3: find the minimal enclosing circle with three points on its boundary
External Links
External Links
Permanent Citation
Permanent Citation
Frederick Wu
"Minimal Enclosing Circle"
http://demonstrations.wolfram.com/MinimalEnclosingCircle/
Wolfram Demonstrations Project
Published: March 7, 2011