Energy Levels of a Morse Oscillator
Energy Levels of a Morse Oscillator
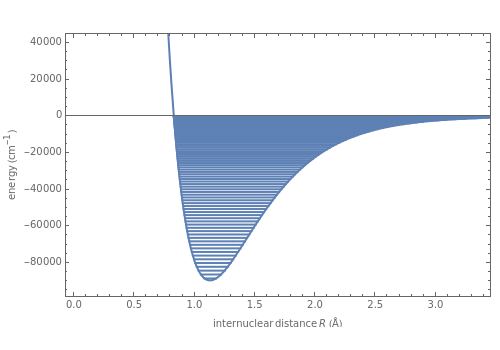
The Morse function , where is the internuclear distance, provides a useful approximation for the potential energy of a diatomic molecule. It is superior to the harmonic oscillator model in that it can account for anharmonicity and bond dissociation. The relevant experimental parameters are the dissociation energy and the fundamental vibrational frequency , both conventionally expressed in wavenumbers (), the equilibrium internuclear distance in Angstrom units (Å), and the reduced mass in atomic mass units (amu). The exponential parameter is given by in appropriate units. The Schrödinger equation for the Morse oscillator is exactly solvable, giving the vibrational eigenvalues =v+-, for . Unlike the harmonic oscillator, the Morse potential has a finite number of bound vibrational levels with ≈2/.
V(R)=(-2)
D
e
-2a(R-)
R
e
e
-a(R-)
R
e
e
R
D
e
ω
e
-1
cm
R
e
μ=/(+)
m
1
m
2
m
1
m
2
a=
ω
e
μ/2
D
e
ϵ
v
ω
e
1
2
2
ω
e
4
D
e
2
v+
1
2
v=0,1,2,...,
v
max
v
max
D
e
ω
e
Details
Details
Snapshot 1: vibrational states of molecule
H
2
Snapshot 2: HCl molecule
Snapshot 3: HI molecule
Reference: P. M. Morse, "Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels," Phys. Rev., 34(1), 1929 pp. 57–64.
External Links
External Links
Permanent Citation
Permanent Citation
S. M. Blinder
"Energy Levels of a Morse Oscillator"
http://demonstrations.wolfram.com/EnergyLevelsOfAMorseOscillator/
Wolfram Demonstrations Project
Published: March 7, 2011