Section 5.1
Section 5.1
To draw a graph in Mathematica, make a list of the edges you want to include, using arrows to indicate which vertices are connected. If you want directed edges, change the code to DirectedEdgesTrue. You get the arrow by typing a dash - then a > symbol.
In[]:=
Graph[{11,21,32,23,41,24},DirectedEdgesFalse]
Out[]=
If you want labels, you can add them. If you set the labels to Automatic, you get, well, automatically generated labels. This isn’t a bad idea if you only want the vertices labelled.
In[]:=
Graph[{11,21,32,23,41,24},VertexLabelsAutomatic,EdgeLabelsAutomatic,DirectedEdgesTrue]
Out[]=
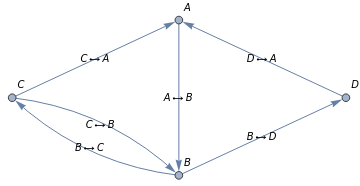
You can also use letters to signify vertices.
In[]:=
samplegraph=Graph[{AB,BC,CA,DA,BD,CB},VertexLabelsAutomatic,EdgeLabelsAutomatic,DirectedEdgesTrue]
Out[]=
Of course, custom labels look nicer!
In[]:=
Graph[{11,21,32,23,41,24},VertexLabels{(1),(2),(3),(4)},EdgeLabels{(11),(21),(32),(23),(41),(24)},DirectedEdgesTrue]
v
1
v
2
v
3
v
4
e
1
e
2
e
3
e
4
e
5
e
6
Out[]=
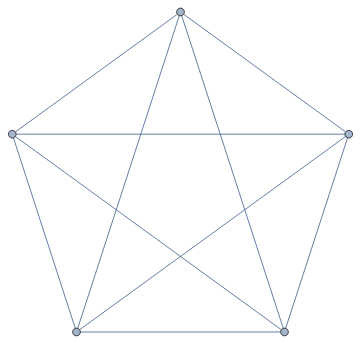
Complete graphs are easy to make...
In[]:=
CompleteGraph[5]
Out[]=
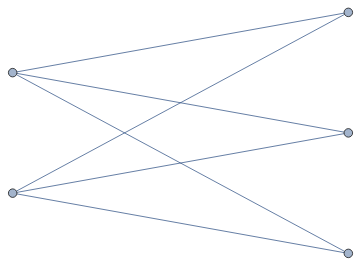
... as are complete bipartite graphs.
In[]:=
CompleteGraph[{2,3}]
Out[]=
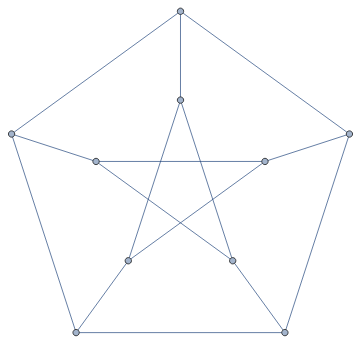
Some really important graphs have their own commands!
In[]:=
PetersenGraph[]
Out[]=
Do you want to see a graph with a specific degree sequence? You can do that! Keep hitting enter below and you’ll see different graphs with the same degree sequence.
In[]:=
degreesequence={5,4,4,3,1,1};RandomGraph[DegreeGraphDistribution[degreesequence],VertexLabelsTable[(i),{i,1,Length[degreesequence]}]]
v
i
Out[]=
Do you want to know whether or not your favorite graph is bipartite? Mathematica can answer that question!
In[]:=
BipartiteGraphQ[samplegraph]
Out[]=
False
BipartiteGraphQ[CompleteGraph[{4,5}]](*Ofcoursethecompletebipartitegraphwith4verticesinonesetand5verticesintheotherisbipartite!*)
True
Section 5.2
Section 5.2
You can also produce adjacency matrices automatically, but only if you have used the Graph command. Why? The Graph command creates a list, but the GraphPlot command creates a graphics object. It’s complicated. We will discuss these later in the course.
In[]:=
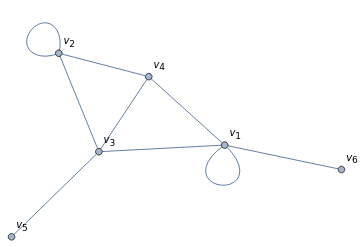
samplegraph3=Graph[{11,61,32,41,24,51,54,35,21,36,46,56},DirectedEdgesFalse,VertexLabels"Name"]
Notice that in the Adjacency matrix, the vertices are renumbered in the order they appear in your Graph statement. If you want to keep them in the traditional order, be careful of the order in which you define your edges. Compare the above to the next couple of cells. All I did was re-order the red entries, and the graph even looks different!
Including the labels in the matrix can help us decipher what the numbers mean. The command below puts headings on the matrix.
To see how many paths of length 7 exist from vertex 2 to vertex 5, we raise the adjacency matrix to the 7th power and check out the corresponding entry in the resulting matrix.
The heading would help here.
There are 1985 paths of length 7 from vertex 2 to vertex 5!
Here is another example using letters to label the vertices.
Here is a little bit of code to find the diameter of a graph. Do you see why each part is there?