Graphs of Exponential Functions

exponential base a

3.95

multiplicative constant C

0.5

zoom

in

default

out

A general exponential function has the form

f(x)=C

x

a

, where

C

and

a

are positive real numbers. The number

a

is called the exponential base and the number

C

is called the multiplicative constant.

If the base

a>1

, then the function is one of exponential growth and the function is always increasing. If the base

a<1

, then the function is one of exponential decay and is therefore always decreasing.

Details

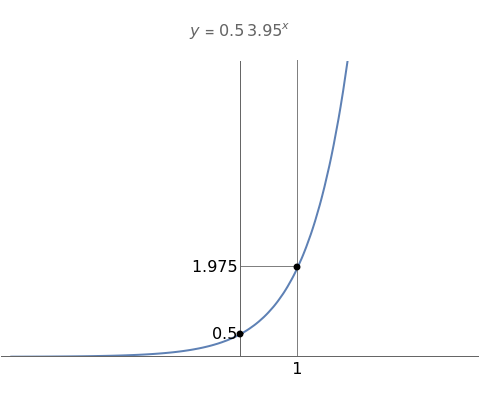
There are two special points to keep in mind to help sketch the graph of an exponential function: At

x=0

, the

y

value is

y=C

0

a

=C

and at

x=1

, the

y

value is

y=C·

1

a

=C·a

.

Here are three other properties of an exponential function:

• The

y

intercept is always at

(0,C)

.

• There are no

x

intercepts. In fact, the exponential function has horizontal asymptote at

y=0.

• The graph is always above the

x

axis.

External Links

Elementary Transcendental Functions and Their Inverses

Continuous Exponential Growth

Exponential Function (Wolfram MathWorld)

Permanent Citation

Laura R. Lynch

"Graphs of Exponential Functions"
http://demonstrations.wolfram.com/GraphsOfExponentialFunctions/
Wolfram Demonstrations Project
Published: June 17, 2014