Relating Trilinear and Tripolar Coordinates for a Triangle
Relating Trilinear and Tripolar Coordinates for a Triangle
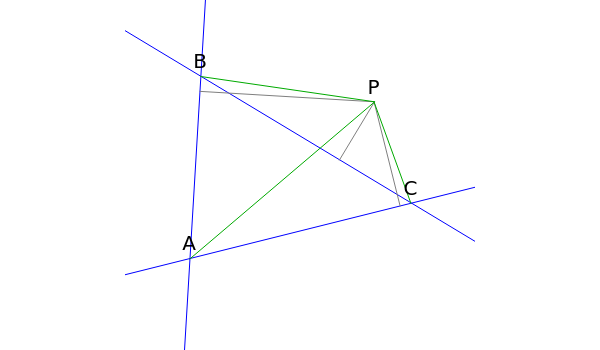
Given a triangle , the trilinear coordinates of a point are the signed distances to the extended sides. Denote the signed distances of to , and by , and , respectively. If and the incenter are in the same half-plane determined by a side, the signed distance to that side is positive; otherwise, it is negative.
ABC
P
P
BC
CA
AB
d
a
d
b
d
c
P
I
The tripolar coordinates of the point are its distances to the vertices of the triangle, given by =PA, =PB and =PC.
P
s
A
s
B
s
C
The Conway triangle notation relates the sides to twice the area of the triangle, denoted by :
S
S
A
2
b
2
c
2
a
2
S
B
2
c
2
a
2
b
2
S
C
2
a
2
b
2
c
2
S=++
S
A
S
B
S
B
S
C
S
C
S
A
These definitions imply the following formulas between the trilinear and tripolar coordinates:
d
a
2
a
S
A
2
AP
S
B
2
CP
S
C
2
BP
2aS
d
b
2
b
S
B
2
BP
S
C
2
AP
S
A
2
CP
2bS
d
c
2
c
S
C
2
CP
S
B
2
AP
S
A
2
BP
2cS
External Links
External Links
Permanent Citation
Permanent Citation
Minh Trinh Xuan
"Relating Trilinear and Tripolar Coordinates for a Triangle"
http://demonstrations.wolfram.com/RelatingTrilinearAndTripolarCoordinatesForATriangle/
Wolfram Demonstrations Project
Published: April 26, 2022