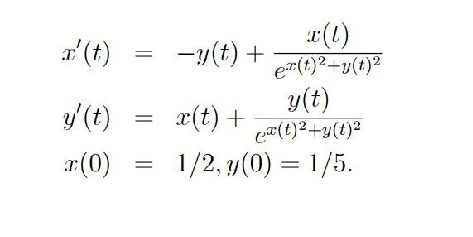Integration problem
Integration problem
The full problem as seen is below, along with the attempts. I’m not sure why only the bottom attempt works.
In[]:=
Attempt 1 with DSolve
Attempt 1 with DSolve
In[]:=
eqns=x'[t]-y[t]+x[t]*,y'[t]x[t]+y[t]*,x[0]12,y[0]15;
--
2
x[t]
2
y[t]
--
2
x[t]
2
y[t]
In[]:=
DSolve[eqns,{x,y},{t,0,1}]
Out[]=
DSolve[t]x[t]-y[t],[t]x[t]+y[t],x[0],y[0],{x,y},{t,0,1}
′
x
--
2
x[t]
2
y[t]
′
y
--
2
x[t]
2
y[t]
1
2
1
5
Attempt 2 with DSolve in a constrained region
Attempt 2 with DSolve in a constrained region
This seems to give a result but with an InterpolatingFunction output.
In[]:=
solsN=NDSolve[eqns,{x,y},{t,0,2}]
Out[]=
xInterpolatingFunction,yInterpolatingFunction
In[]:=
solsN[[1]]
Out[]=
xInterpolatingFunction,yInterpolatingFunction
In[]:=
Plot[{x[t],y[t]}/.solsN,{t,0,2}]
Out[]=