Cnoidal Waves from Korteweg-de Vries Equation
Cnoidal Waves from Korteweg-de Vries Equation
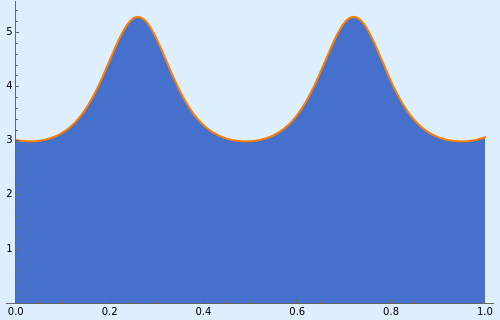
A cnoidal wave is an exact periodic traveling-wave solution of the Korteweg–de Vries (KdV) equation, first derived by them in 1895. Such a wave describes surface waves whose wavelength is large compared to the water depth.
Details
Details
The surface elevation of a cnoidal wave takes the form
η(x,t)=+H
η
2
2
cn(2/λK(m)(x-ct)m)
where is the elevation, is the wave height, is the phase velocity (the rate at which the phase of the wave propagates), is the wavelength, and is the Jacobi elliptic function (hence the name cnoidal). is the complete elliptic integral of the first kind, with being the elliptic parameter that for large values produces smoother troughs and more pronounced crests than in the case of a sine wave.
η
2
H
c
λ
cn
K(m)
m
References
References
External Links
External Links
Permanent Citation
Permanent Citation
Enrique Zeleny
"Cnoidal Waves from Korteweg-de Vries Equation"
http://demonstrations.wolfram.com/CnoidalWavesFromKortewegDeVriesEquation/
Wolfram Demonstrations Project
Published: May 28, 2013