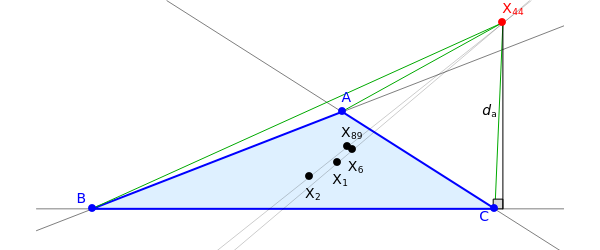
Basic Parameters of the Kimberling Center X(44)
Basic Parameters of the Kimberling Center X(44)
Given a triangle , the Kimberling center is the intersection of the lines (incenter-symmedian point) and (centroid-Kimberling center )[1].
ABC
X
44
X
1
X
6
X
2
X
89
X
89
The Kimberling center is the isogonal conjugate of [1].
X
89
X
45
Let
a
b
c
R
r
s
ABC
d
a
d
b
d
c
X
44
ABC
d
X
44
d
a
d
b
d
c
Then
=(3+12rR+)-2as(3+6rR+)-3r(4R+r)+
AX
44
2
a
2
r
2
s
2
r
2
s
2
s
-9-9(-4)+r(r-12R)+
3
r
3
(r+4R)
2
r
2
r
2
R
2
s
4
s
6
s
2
(-3r(r+4R)+)
2
s
d
a
rs(2s-3a)
3r(4R+r)-
2
s
d
X
44
You can drag the vertices , and .
A
B
C
Details
Details
A triangle center is said to be even when its barycentric coordinates can be expressed as a function of three variables , , that all occur with even exponents. If the center of a triangle has constant barycentric coordinates, it is called a neutral center (the centroid is the only neutral center). A triangle center is said to be odd if it is neither even nor neutral.
a
b
c
X
2
Standard barycentric coordinates of a point with respect to a reference triangle have a sum of 1.
References
References
[1] C. Kimberling. "Encyclopedia of Triangle Centers." (Nov 17, 2022) faculty.evansville.edu/ck6/encyclopedia.
External Links
External Links
Permanent Citation
Permanent Citation
Minh Trinh Xuan
"Basic Parameters of the Kimberling Center X(44)"
http://demonstrations.wolfram.com/BasicParametersOfTheKimberlingCenterX44/
Wolfram Demonstrations Project
Published: November 28, 2022