Basic Parameters of the Symmedian Point
Basic Parameters of the Symmedian Point
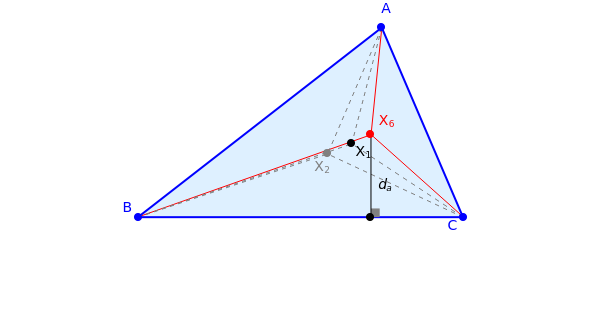
The angle bisectors of a triangle intersect at the incenter . The isogonal conjugate of a point is found by reflecting the lines , , about the angle bisectors. The symmedian point [1] of is the isogonal conjugate of the centroid .
ABC
X
1
-1
P
P
AP
BP
CP
X
6
ABC
X
2
Let
d
a
d
b
d
c
X
6
ABC
d
X
6
d
a
d
b
d
c
a
b
c
s
ABC
S=2ABC
S
A
S
B
S
C
S
θ
ω
Then, it can be shown that
=
AX
6
bc
2(+)-
2
b
2
c
2
a
2
S
ω
d
a
aS
2
S
ω
d
X
6
sS
S
ω
You can drag the vertices , and .
A
B
C
Details
Details
A triangle center is said to be even when its barycentric coordinates can be expressed as a function of three variables , , that all occur with even exponents. If the center of a triangle has constant barycentric coordinates, it is called a neutral center (the centroid is the only neutral center). A triangle center is said to be odd if it is neither even nor neutral.
a
b
c
X
2
Standard barycentric coordinates of a point with respect to a reference triangle are normalized to a sum of 1.
References
References
[1] C. Kimberling. "Encyclopedia of Triangle Centers." (Aug 15, 2022) faculty.evansville.edu/ck6/encyclopedia.
External Links
External Links
Permanent Citation
Permanent Citation
Minh Trinh Xuan
"Basic Parameters of the Symmedian Point"
http://demonstrations.wolfram.com/BasicParametersOfTheSymmedianPoint/
Wolfram Demonstrations Project
Published: August 26, 2022