Hyperbolic Triangle
Hyperbolic Triangle
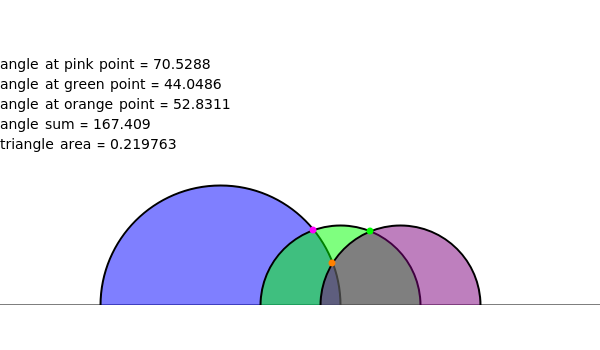
Using three semicircles, this Demonstration creates a hyperbolic triangle, measures and totals its angles, and calculates its area using the Gauss–Bonnet formula. You can vary the radii of the circles, thus changing all the measurements.
Details
Details
In the upper half-plane model of hyperbolic geometry, the hyperbolic straight lines are the vertical rays and the semicircles touching the axis.
x
The measure of the angle formed by the intersection of two semicircles is calculated by measuring the angle of the tangents to the circles at that point. The angle sum of a hyperbolic triangle is less than 180 degrees.
The Gauss–Bonnet formula states that the area of a hyperbolic triangle is the difference of (or 180°) and the sum of the interior angles of the triangle.
π
References
References
R. E. Schwartz, "Ideal Triangle Groups, Dented Tori, and Numerical Analysis," Annals of Mathematics, 153, 2001 pp. 533–598.
External Links
External Links
Permanent Citation
Permanent Citation
Michael Rach, Ron Grosz
"Hyperbolic Triangle"
http://demonstrations.wolfram.com/HyperbolicTriangle/
Wolfram Demonstrations Project
Published: March 7, 2011