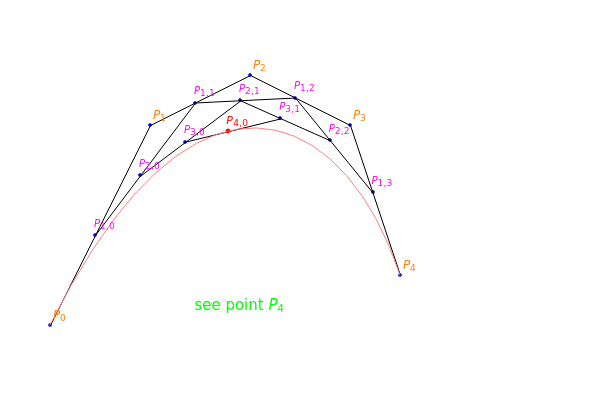
Generating a Bezier Curve by the de Casteljau Algorithm
Generating a Bezier Curve by the de Casteljau Algorithm
This Demonstration shows how to generate a Bezier curve by the de Casteljau algorithm. An -degree Bezier curve is defined by
th
n
C(u)=(u)
n
∑
i=0
B
i,n
P
i
B
i,n
n!
i!(n-i)!
n-i
i
u
0≤u≤1
Consider linked segments. For each, use a percentage index to indicate a point at that percentage of the segment's length. Use these points to make segments, and repeat using the same index. More formally, define a basis function:
n
u
n-1
B
i,n
n!
i!(n-i)!
n-i
i
u
(n-1)!n
i!(n-i)!
n-i
i
u
(n-1)!
i!(n-i)!
n-i
i
u
(n-1)!
i!(n-i)!
n-i
i
u
(n-1)!
i!(n-i)!
n-i
i
u
(n-1)!
i!(n-i-1)!
n-i
i
u
(n-1)!
(i-1)!(n-i)!
n-i
i
u
(n-1)!
i!(n-i-1)!
n-1-i
i
u
(n-1)!
(i-1)![(n-1)-(i-1)]!
(n-1)-(i-1)]
i-1
u
B
i,n-1
B
i-1,n-1
Denoting a general -degree Bezier curve by (,,⋯,), we have
th
n
C
n
P
0
P
1
P
n
C
n
P
0
P
n
C
n-1
P
0
P
n-1
uC
n-1
P
1
P
n
This follows from the recursive definition of the basis function.
Fixing and denoting by , this yields a recursive algorithm for computing the point on an -degree Bezier curve, that is,
u=
u
0
P
i
P
0,i
C()=()
u
0
P
n,0
u
0
th
n
P
k,i
u
0
u
0
P
k-1,i
u
0
u
0
P
k-1,i+1
u
0
k=1,…,n
i=0,…,n-k
This is called the de Casteljau algorithm.
References
References
[1] L. Piegl and W. Tiller, The NURBS Book, 2nd ed., Berlin: Springer-Verlag, 1997 pp. 9–10, 23–24.
Permanent Citation
Permanent Citation
Shutao Tang
"Generating a Bezier Curve by the de Casteljau Algorithm"
http://demonstrations.wolfram.com/GeneratingABezierCurveByTheDeCasteljauAlgorithm/
Wolfram Demonstrations Project
Published: November 7, 2014