CDF 실험문서의 Enterprise & Cloud 배포
파주여고 이장훈
mathought@gmail.com
CDF는 수학교육 콘텐츠 배포를 위한 좋은 도구이지만, Wolfram Player에서 동작하는데 몇 가지 제한이 있다. Enterprise CDF는 InputField에서 string을 지원하고, 데이터 입출력 등 모든 기능의 사용이 가능하다. Cloud CDF는 Wolfram Player가 미설치된 태블릿, 모바일에서도 동작이 가능하다. 우리는 CDF 예제를 통하여 세 가지 배포 방식에 대한 장단점을 이해할 수 있다.
1
.
CDF 문서의 배포 방법
1
.
1
.
CDF
환경 : Wolfram Player가 설치된 PC
장점 : Mathematica 수준의 계산속도 및 즉각적인 반응
단점 : String InputFiled, Import & Export 등 일부 기능의 사용 제한, 태블릿 & 모바일 미지원
1
.
2
.
Enterprise CDF
환경 : Wolfram Player가 설치된 PC
장점 : Mathematica 수준의 계산속도 및 즉각적인 반응, String InputFiled, Import & Export 지원
단점 : 고가의 Enterprise Mathematica 라이선스, 태블릿 & 모바일 미지원
1
.
3
.
Wolfram Cloud CDF
환경 : 모든 디바이스에서 SW설치 없이 동작 장점 : 태블릿 & 모바일에서 동작, String InputFiled, Import & Export 기능 지원단점 : webMathematica 수준의 더딘 계산 및 컨트롤 반응 속도교실 수업에서 학급 구성원(20명 이상) 동시접속의 버겨움 명확하지 않은 오류, 내장함수 지원여부 등의 문제 발생시 디버그 작업과정이 어려움​
​​
2
.
CDF 콘텐츠 배포 및 활용 사례
2
.
1
.
CDF vs Enterprise CDF vs Cloud webCDF
세가지 배포형식 CDF, Enterprise CDF, Cloud webCDF에 대한 실험문서를 비교해보자.
◼
  • 그래프 스케치북
    • 2
    .
    2
    .
    Enterprise CDF 활용 사례
    파주여고는 Mathematica가 설치된 실습실이 구축되어 있지만,
    타교에서는 공개SW, Wolfram Player를 이용하여 콘텐츠 동작이 가능해야 한다.
    2
    .
    2
    .
    1
    .
    자율교육과정 : 인공지능 체험활동
    ◼
  • 인공지능 자율주행차 시스템 구현 체험
    • ◼
  • 인공지능 가위바위보 EYE 시스템 구현 체험
    • ◼
  • 인공지능 필기체 숫자인식 시스템 구현 체험
    • 2
    .
    3
    .
    Cloud webCDF 활용 사례
    학생들의 스마트 학습도구는 데스크탑 → 노트북 → 태블릿 → 스마트폰으로 이동하였다.
    학생들은 디바이스의 즉각적인 활용이 가능한 스마트폰으로 할 수 있는 교육콘텐츠를 더욱 선호한다.
    2
    .
    3
    .
    1
    .
    자율교육과정 : 인공지능 체험활동
    ◼
  • 인공지능 가위바위보 Brain 체험
    • ◼
  • 인공지능이 그린 그림Ⅰ(ImageRestyle) 체험
    • ◼
  • 인공지능이 그린 그림Ⅱ(Portrait Sketch) 체험
    • ◼
  • 인공지능이 그린 그림Ⅲ(Image from Text) 체험
    • ◼
  • 인공지능이 그린 그림Ⅳ(Quick Hand Sketch) 체험
    • 2
    .
    3
    .
    2
    .
    정규교육과정 : 공학계산 + 게임수학 + 시뮬레이션
    ◼
  • 공학계산 : 이항분포 & 정규분포 계산기
    • ◼
  • 게임수학 : NIM 게임, 하노이 탑(실험+정답), 서바이벌 Deal or No Deal 게임
    • ◼
  • 시뮬레이션 : 로또복권 & 번호확장, 원주율 탐색, 심볼아트, 팬데믹 방역효과
    • 2
    .
    3
    .
    3
    .
    심화교육과정 : 공학프로그램 webMathematica
    ◼
  • 최신 버전의 간단한 Mathematica 코드의 작성과 출력, 만델브로 집합
    • ◼
  • 다항식으로 표현된 정폭도형의 방정식 찾기 (과학고 학생 R & E 자문 사례)
    • In[1]:=
    a=2;b=8;​​
    p[t_]:=a
    2
    Cos3
    t
    2
    
    +b;
    ​​
    xt=p[t]Cos[t]-p'[t]Sin[t];
    ​​
    yt=p[t]Sin[t]+p'[t]Cos[t];
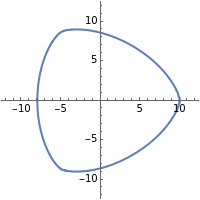
    ​​ParametricPlot[{xt,yt},{t,0,2Pi},PlotRange->{{-12,12},{-12,12}},ImageSize->200]
    Out[5]=
    In[6]:=
    xt=p[t]Cos[t]-p'[t]Sin[t]
    ​​xt=TrigReduce[xt]​​xt=TrigExpand[xt]​​xt=xt/.
    n_
    Sin[t]
    ->
    n
    2
    (1-
    2
    Cos[t]
    )
    ​​xt=Expand[xt]​​xt=xt/.Cos[t]->c
    Out[6]=
    Cos[t]8+2
    2
    Cos
    3t
    2
    
    +6Cos
    3t
    2
    Sin[t]Sin
    3t
    2
    
    Out[7]=
    9Cos[t]+2Cos[2t]-Cos[4t]
    Out[8]=
    9Cos[t]+2
    2
    Cos[t]
    -
    4
    Cos[t]
    -2
    2
    Sin[t]
    +6
    2
    Cos[t]
    2
    Sin[t]
    -
    4
    Sin[t]
    Out[9]=
    9Cos[t]+2
    2
    Cos[t]
    -
    4
    Cos[t]
    -2(1-
    2
    Cos[t]
    )+6
    2
    Cos[t]
    (1-
    2
    Cos[t]
    )-
    2
    (1-
    2
    Cos[t]
    )
    Out[10]=
    -3+9Cos[t]+12
    2
    Cos[t]
    -8
    4
    Cos[t]
    Out[11]=
    -3+9c+12
    2
    c
    -8
    4
    c
    In[12]:=
    yt=p[t]Sin[t]+p'[t]Cos[t];
    ​​yt=TrigReduce[yt]​​yt=TrigExpand[yt]​​yt=TrigExpand[yt]/.
    n_
    Sin[t]
    ->
    n
    2
    (1-
    2
    Cos[t]
    )
    ​​yt=yt/.1-
    2
    Cos[t]
    ->
    2
    Sin[t]
    ​​yt=yt/.{Cos[t]->c,Sin[t]->s}//PowerExpand//Factor
    Out[13]=
    9Sin[t]-2Sin[2t]-Sin[4t]
    Out[14]=
    9Sin[t]-4Cos[t]Sin[t]-4
    3
    Cos[t]
    Sin[t]+4Cos[t]
    3
    Sin[t]
    Out[15]=
    4Cos[t]
    3/2
    (1-
    2
    Cos[t]
    )
    +9Sin[t]-4Cos[t]Sin[t]-4
    3
    Cos[t]
    Sin[t]
    Out[16]=
    9Sin[t]-4Cos[t]Sin[t]-4
    3
    Cos[t]
    Sin[t]+4Cos[t]
    3/2
    (
    2
    Sin[t]
    )
    Out[17]=
    s(9-4c-4
    3
    c
    +4c
    2
    s
    )
    In[18]:=
    eq1=x==xt​​eq2=
    2
    y
    ==Expand[
    2
    yt
    /.
    2
    s
    ->1-
    2
    c
    ]
    Out[18]=
    x-3+9c+12
    2
    c
    -8
    4
    c
    Out[19]=
    2
    y
    81-81
    2
    c
    -144
    3
    c
    +144
    5
    c
    +64
    6
    c
    -64
    8
    c
    In[20]:=
    eq=Eliminate[{eq1,eq2},c]
    Out[20]=
    -373248000+7950960
    2
    x
    +266382
    3
    x
    -41283
    4
    x
    -5544
    5
    x
    +19
    6
    x
    +16
    7
    x
    +
    8
    x
    +7950960
    2
    y
    -799146x
    2
    y
    -82566
    2
    x
    2
    y
    +11088
    3
    x
    2
    y
    -519
    4
    x
    2
    y
    -16
    5
    x
    2
    y
    +4
    6
    x
    2
    y
    -41283
    4
    y
    +16632x
    4
    y
    +441
    2
    x
    4
    y
    -80
    3
    x
    4
    y
    +6
    4
    x
    4
    y
    -45
    6
    y
    -48x
    6
    y
    +4
    2
    x
    6
    y
    +
    8
    y
    0
    In[21]:=
    ContourPlot[Evaluate@eq,{x,-12,12},{y,-12,12},Frame->False,Axes->True,ImageSize->200]
    Out[21]=