Why Density Change Cannot Be Ignored in a Plug Flow Reactor (PFR)
Why Density Change Cannot Be Ignored in a Plug Flow Reactor (PFR)
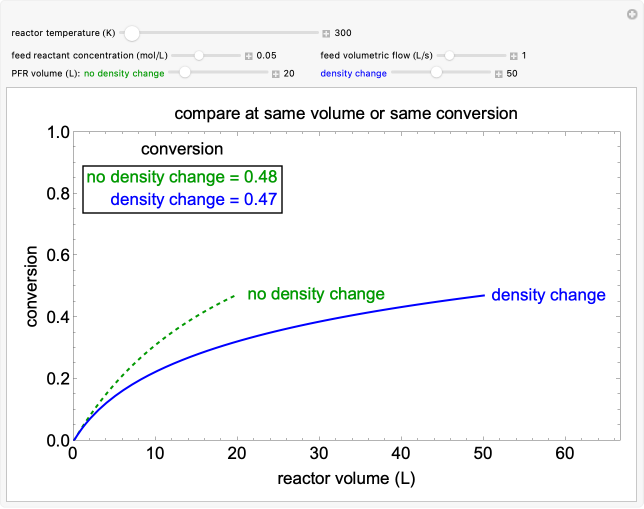
This Demonstration calculates conversion as a function of reactor volume for a second-order, gas-phase reaction in an isothermal, isobaric, plug flow reactor (PFR). The number of moles increases as conversion increases for the reaction , and this causes the mass density to decrease. Thus, the volumetric flow rate increases down the reactor so that the conversion (blue line) is lower than what would be obtained if the mass density were assumed constant (dashed green line). A higher volumetric flow rate means a shorter residence time. Use sliders to change the volumes of the reactor with and without density change in order to make comparisons at the same conversion or the same reactor volume. Use sliders to change the feed reactant concentration, feed volumetric flow rate, and reactor temperature.
A2B+C
Details
Details
Material balances are done to determine the conversion :
x
F
A
V
2
C
A
F
B
V
2
C
A
F
C
V
2
C
A
x=-
F
A,0
F
A
F
A,0
k=
k
o
-
E
a
RT
e
where is the molar flow rate of component , is the rate constant, is volume, = is the feed flow rate of , is the constant volumetric flow rate, is the pre-exponential factor, is the ideal gas constant, and is temperature.
F
i
i=(A,B,C)
k
V
F
A,0
v
0
C
A,0
A
v
0
k
o
R
T
When density change is ignored, the concentration of is:
A
C
A
C
A
F
A
v
0
When density change is taken into account:
C
A
F
A
v
v=++
F
A
F
B
F
C
C
A,0
where is volumetric flow rate, which changes with distance down the reactor.
v
The screencast video at[1] show how to use this Demonstration.
References
References
[1] Why Density Change Cannot Be Ignored in a Plug Flow Reactor (PFR). www.colorado.edu/learncheme/kinetics/CantIgnoreDensityPFR.html.
Permanent Citation
Permanent Citation
Rachael L. Baumann, John L. Falconer
"Why Density Change Cannot Be Ignored in a Plug Flow Reactor (PFR)"
http://demonstrations.wolfram.com/WhyDensityChangeCannotBeIgnoredInAPlugFlowReactorPFR/
Wolfram Demonstrations Project
Published: July 29, 2013