In[]:=
RandomGraph[{10,20},DirectedEdgesTrue]
Out[]=
In[]:=
TransitiveClosureGraph
Out[]=
In[]:=
Graph[Join[EdgeList[%],##&/@VertexList[%]]]
Out[]=
In[]:=
LayeredGraphPlot[%]
Out[]=
In[]:=
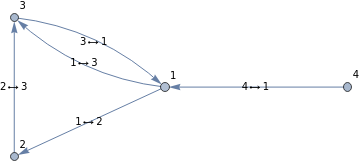
RandomGraph[{3,5},DirectedEdgesTrue,VertexLabelsAutomatic,EdgeLabels"Name"]
Out[]=
In[]:=
RandomGraph[{4,5},DirectedEdgesTrue,VertexLabelsAutomatic,EdgeLabels"Name"]
Out[]=
In[]:=
PathGraph[Range[4],DirectedEdgesTrue,VertexLabelsAutomatic]
Out[]=
In[]:=
PathGraph[Range[5],DirectedEdgesTrue,VertexLabelsAutomatic]
Out[]=
Category of graphs...
graph cat
int,list
list[int]
list[list[int]]
f[int]int(*type:intint*)
g[int]list[int]
morphisms :
identity morphism :
f[int]int
g[f[int]]:intintlist[int]
int int
set set
set of morphisms between objects ; can you represent that set as itself a member of the category (-> closed category)
expr
f[g[x_],y_]h[x,y]
closed categories ↔ programs=data
In[]:=
AxiomaticTheory["GroupAxioms"]
Out[]=
a.⊗(b.⊗c.)(a.⊗b.)⊗c.,a.⊗a.,a.⊗
∀
{a.,b.,c.}
∀
a.
1
∀
a.
a.
1
In[]:=
CayleyGraph[AlternatingGroup[4]]
Out[]=
In[]:=
TransitiveClosureGraph[%]
Out[]=
sieve
Lawvere-Tierney
state vertex is like an open set
λ a λ b .