In[]:=
ClearAll
Out[]=
ClearAll
In[]:=
f[x_]:=(x^2+x+1)/(x-1)
In[]:=
D[f[x],x]
Out[]=
1+2x
-1+x
1+x+
2
x
2
(-1+x)
In[]:=
Plot[f[x],{x,-4,4}]
Out[]=
In[]:=
sol=Solve[D[f[x],x]==0,x]
Out[]=
{x1-
3
},{x1+3
}In[]:=
FullSimplify[f''[x]/.sol]
Out[]=
-,
2
3
2
3
In[]:=
Plot[f[x],{x,-5,5},Epilog{Red,PointSize[Large],Point[{x,f[x]}/.sol]},AspectRatioAutomatic]
Out[]=
In[]:=
sol1=Solve[D[f[x],{x,2}]==0,x]
Out[]=
{}
In[]:=
cp=Reduce[D[f[x],{x,2}]>0]
Out[]=
x>1
In[]:=
cn=Reduce[D[f[x],{x,2}]<0]
Out[]=
x<1
In[]:=
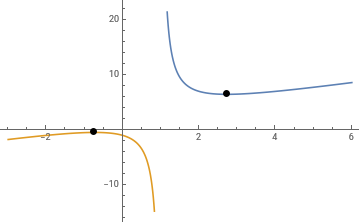
Plot[{Piecewise[{{f[x],cp}},Undefined],Piecewise[{{f[x],cn}},Undefined]},{x,-3,6},Epilog{PointSize[Large],Point[{x,f[x]}/.sol]},PlotLegendsLineLegend[{"wypukle","wklesle"}]]
Out[]=