Successive Differences of Sequences
Successive Differences of Sequences
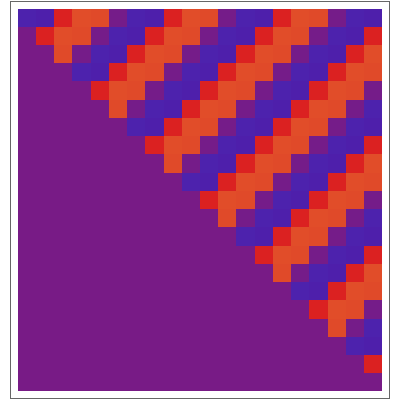
Let be a sequence of numbers ,,,,,…. In this Demonstration the sequences are named integer sequences.
s
a
1
a
2
a
3
a
4
a
5
The sequence of differences of is a new sequence -,-,-,-,….
s
Δ(s)=
a
2
a
1
a
3
a
2
a
4
a
3
a
5
a
4
For example, the sequence of differences of the sequence is . The second differences are the differences of the differences, in this case .
1,3,9,27,81,243,…
2,6,18,54,162,486,…
4,12,36,108,324,972,…
In the graphic, numbers are coded by color. Each row consists of the differences of the row above it, shifted over by one each time. In symbols, the first row is the sequence ; the second row is the sequence ; the third row is ; and so on.
s
Δ(s)
Δ(Δ(s))=(s)
2
Δ
Taking differences is the first thing to try when investigating a sequence.
Details
Details
The sequence is often written more compactly as , in analogy with , the infinite sum of the sequence . The notions of sequence and series are related but often mixed up by beginners; sequences are indexed sets of numbers and series add them up. Of course, the sums of integer sequences such as the ones in this Demonstration do not converge in the usual sense.
s
s=
∞
{}
a
i
i=1
∞
Σ
i=1
a
i
s
External Links
External Links
Permanent Citation
Permanent Citation
George Beck
"Successive Differences of Sequences"
http://demonstrations.wolfram.com/SuccessiveDifferencesOfSequences/
Wolfram Demonstrations Project
Published: March 7, 2011