THESE FIRST FEW CELLS (WHICH LOOK EMPTY) CONTAIN THE CODE FOR THE COMMANDS USED BELOW. I WOULDN'T RECOMMEND DELETING THEM. YOU ARE WELCOME TO TAKE A LOOK THOUGH!
In[1]:=
iterate[functmm_,startmm_, itmm_,skipmm_]:=
MatrixForm[N[NestList[functmm,Nest[functmm,N[startmm],skipmm],itmm],10]]
MatrixForm[N[NestList[functmm,Nest[functmm,N[startmm],skipmm],itmm],10]]
In[2]:=
iterateexact[functmm_,startmm_, itmm_,skipmm_]:=
MatrixForm[NestList[functmm,Nest[functmm,startmm,skipmm],itmm]]
MatrixForm[NestList[functmm,Nest[functmm,startmm,skipmm],itmm]]
In[3]:=
f[x_] := 4 x(1-x); (*This is the function we will be examining in detail.*)
To iterate a calculator button, choose one of the cells below and evaluate it. Only the most recently evaluated function will be iterated. See the iterate command below.
f[x_]:=x^2
In[6]:=
f[x_]:=Sin[x]
f[x_]:=Cos[x]
f[x_]:=ArcTan[x]
In[4]:=
f[x_]:=Sqrt[x]
a=4;
Plot[{f[x],x, 1}, {x,0,1}, PlotRange->All]
a=4;
Plot[{f[x],x, 1}, {x,0,1}, PlotRange->All]
Out[14]=
You can also solve the equation , or use FindRoot if the Solve command can't handle it.
f(x)=x
In[13]:=
a=4;
Solve[f[x]==x,x]
Solve[f[x]==x,x]
Out[14]=
{x0},x
3
4
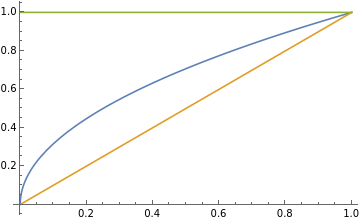
A periodic point of period is a point satisfying (p)=p, and the point is said to be of least period if (p)p for all The methods described above can also work for points of higher period. I have included an example of a search for period 3 points. To find points of period 3, we set f(f(f(x)))=x and solve for x. The Mathematica command for (x) is Nest[f,x,3]. The graph below shows the line , , and .
n
p
n
f
n
k
f
0<k<n.
3
f
y=x
y=f(x)
y=(x)
3
f
In[15]:=
a=4;
Plot[{Nest[f,x,4],f[x],x}, {x,0,1}, PlotRange->{0,1}]
Plot[{Nest[f,x,4],f[x],x}, {x,0,1}, PlotRange->{0,1}]
Out[16]=
In[21]:=
a=4;
iterate[f,.123,10,100]
iterate[f,.123,10,100]
Out[22]//MatrixForm=
0.84197 |
0.532227 |
0.995846 |
0.0165479 |
0.0650963 |
0.243435 |
0.736698 |
0.775896 |
0.695526 |
0.847079 |
0.518145 |
Sometime we want to iterate exact values. Don't use this command unless you know that's what you want to do.
In[23]:=
a=4;iterateexact[f,6/50,5,0]
Out[24]//MatrixForm=
3 25 |
264 625 |
381216 390625 |
14347445376 152587890625 |
7933588947855784874496 23283064365386962890625 |
487105714111637651321687114011451962114983936 542101086242752217003726400434970855712890625 |
Why not use iterateexact all the time? That’s obvious from the last line. Note that if we left the input as 0.12 Mathematica would use decimal approximations.
In[92]:=
a=4;iterateexact[f,6/50.,5,0]
Out[93]//MatrixForm=
0.12 |
0.4224 |
0.975913 |
0.0940274 |
0.340745 |
0.898551 |